INTRODUCTION
The manager needs various techniques to assist and help him in making decisions that will ultimately maximise the value of the firm. These techniques and tools are quantitative in nature. The introduction of some commonly used tools used in
managerial decision making becomes imperative.

In this unit we are going to discuss some basic techniques which would be helpful in understanding the concept of managerial economics, in turn helping us to apply these techniques as and when required.

OPPORTUNITY SET
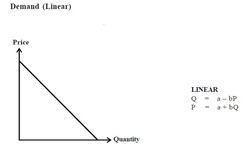
A set is a collection of distinct or well defined objects like (5, 6, 7) or (a, b, c). For example listing of all residents of Delhi or all animals in a zoo is difficult. Thus a set is also formed by developing a criterion for membership. For example the set of all positive numbers between 1 and 10 or set of all points lying on the line x + y = 4. In managerial economics the need is to define an opportunity set of a decision maker, i.e., the set of alternative actions which are feasible. For example, the opportunity set of a consumer is the set of all combinations of goods which the consumer can buy with his given income. Given the consumer’s budget and prices of all goods, the opportunity set is well defined, and we can find out whether the Five key functions of economics are represented graphically:

DERIVATIVES

The “slope” in mathematical use is the concept of ‘marginalism’ in economic use. Thus if Y=Y(x), dy/dx stands for change in Y as a result of one unit change in X, i.e. marginal y of x. This slope or marginal function has enormous use in managerial economics. Thus,

PARTIAL DERIVATIVES

In managerial economics, usually a function of several independent variables is encountered instead of a single variable case shown above. For example, a consumer’s demand for a product depends on the price of the product, price of
other related goods, income, tastes, etc. When price changes, the effect on quantity demanded of the goods can be analysed only when all other variables are kept constant. The functional relationship that is obtained between the quantity
demanded of a product and its own price is called a Partial Function (a function of one variable when all other variables are kept constant). The derivative of the partial functions are known as partial derivatives of the original function and is
shown as df/dx1 or f1(x) or f’(x). The conventional symbol used in maths for the partial derivative is delta, d. Partial derivatives are functions of all variables entering into the original function f (x).

OPTIMISATION CONCEPT

Optimisation is the act of choosing the best alternative out of the available ones. It describes how decisions or choices among alternatives are taken or should be made. All such optimisation problems have 3 elements:

a) Decision Variables: These are variables whose optimal values have to be determined. For example, a production manager wants to know at what level to set output in order to achieve maximum profit or maximum sales revenue. Here
output is the decision or choice variable. Similarly labour, machine, time and raw materials are choice variables if a works manager wants to know what amount of these are to be used so as to produce a given output level at minimum cost.
The quantity of any choice variable must be measurable (20kg, 5 labourers, 10 hours, etc.).

b) The Objective Function: It is a mathematical relationship between the choice variables and some variables whose values are to be maximised or minimised.
For example, the objective function could relate profit to level of output or cost to amount of labour, machine, time, raw materials, etc. in the above example.

c) The Feasible Set: The available set of alternatives is called a feasible set. A solution to an optimisation problem is that set of values of the choice variables which is in the feasible set and which yields maximum or minimum of the objective
function over the feasible set.

Unconstrained Optimisation Technique

For unconstrained optimisation problem involving single independent variable, we need to satisfy some “conditions”. In economics, the necessary (first order) condition is called the equilibrium condition and sufficient (second order) condition is called the stability condition (continuation of state of equilibrium). There may be equilibrium but it may not be stable.

Constrained Optimisation Technique

There are many situations where the objective function has to be maximised or minimised subject to certain constraints present in the problem. Thus a consumer may be maximising utility subject to the income constraint. The techniques used to analyse such problems are based on that used for unconstrained problems. The constrained problem is converted into unconstrained one with the help of Lagrange Multiplier Technique and then the latter is solved. In this technique, the objective function and constraint is combined in one expression (Lag range expression) such that the constrained maximisation or minimisation problems are reduced to unconstrained ones.

REGRESSION ANALYSIS

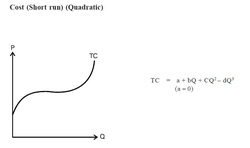
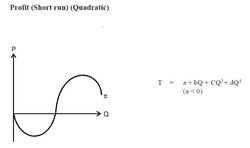
A manager must often determine the total cost of producing various levels of output. The relation between total cost (C) and quantity (Q) is, C = a + bQ + cQ2 + dQ3 Where a, b, c and d are parameters of the equation. Parameters are coefficients in an equation that determine the exact mathematical relation among the variables in the equation. If the numerical values of parameters are determined, the manager knows the quantitative relation between output and total cost. If the value of parameters of cost equation are calculated to be a = 1262, b = 1, c = –0.03 and d = 0.005, the equation becomes, C = 1262 + 1Q –0.03Q2 + 0.005Q3

This equation can be used to compute the total cost of producing various levels of output. If, for example, the manager wishes to produce 30 units of output, the total cost can be calculated as C = 1262 + 30 –0.03(30)2 + 0.005(30)3 = Rs. 1400.

Thus, in order for the cost function to be useful for decision making, the manager must know the numerical value of the parameters.

The values of the parameters are often obtained by using a technique called regression analysis. It determines the mathematical relation between a dependent variable and one or more explanatory variables.

• Dependent variable: The variable whose variation is to be explained.

• Explanatory variables: The variables that are thought to cause the dependent variable to take on different values.

In the simple regression model, the dependent variable Y is related to only one explanatory variable X, and the relation between X and Y is linear:
Y = a + bX

This is the equation for a straight line, with X plotted along the horizontal axis and Y along the vertical axis. The parameter a is called the intercept parameter because it gives the value of Y at the point where the regression line crosses the Y-axis. (X is equal to zero at this point). The parameter b is called the slope parameter because
it gives the slope of the regression line. The slope of a line measures the rate of change in Y as X changes (DY/DX); it is therefore the change in Y per unit change in X.

SPECIFYING THE REGRESSION EQUATION

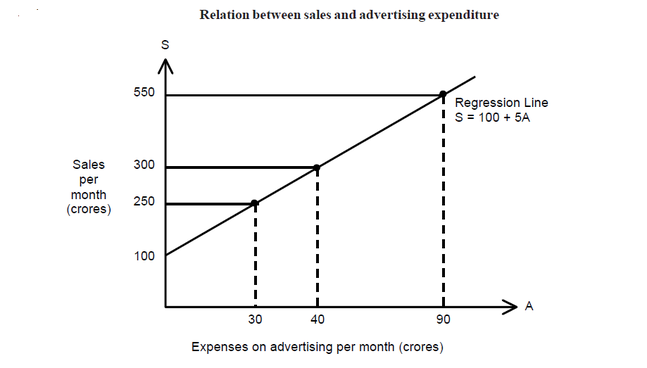
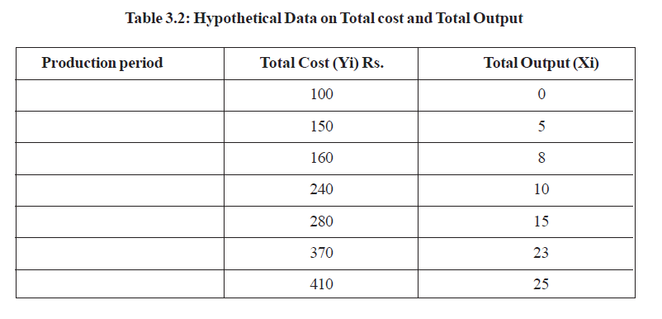
The first thing that the organisation carrying out the regression analysis needs to do is to determine the range of variables which may affect demand for the product concerned. For example, the own price of a good might reasonably be expected to be a determinant of demand for most products, as would any advertising being done by the firm. The question of whether there are any substitute or complementary goods which need to be taken into account could then be raised. In the case of, an expensive consumer durable good, the cost and availability of credit might be a consideration. Any special ‘other’ factors affecting demand could then be identified and so on. This choice of variables has to be made before it is possible to progress to the next stage.

Data Collection

Once the relevant variables have been identified, quantitative data need to be assembled for each of them. This will be easier for some of the variables than for others. In dealing with an established product, for example, the firm might
reasonably be expected to have access to a range of information regarding the variables which it controls such as own price and advertising. What may be more difficult to obtain, however, is information about competitors’ products. On this front, price data can be obtained through observing retail prices, as this information by definition is in the public domain and cannot be hidden. This requires continued market observation, perhaps over a long period of time. Likewise, information about product design changes can be obtained by buying the competitors’ product(s), but this may be expensive if there are many on the market. Confidential, commercially sensitive information such as actual advertising expenditure by competitors and their proposed new products present much more difficult problems in terms of
access and may have to be left out of the process altogether. Data on levels of disposable income, population variables, interest rates and credit availability are easier to obtain, for example from government statistics, but other variables are
more problematic. How can things like expectations and tastes be measured for instance? In these cases the available data, perhaps resulting from market surveys, may be qualitative rather than quantitative. Some means of conversion need to be found if they are to be included in the regression analysis at all. These are the things which the decision maker needs to keep in mind while collecting and selecting data on the relevant variables. Once the first two steps have been
completed, the next stage is to specify the likely form of the regression equation. There are two main forms which are used in practice -the linear demand function and the non-linear or power function. Both treat the demand for the product as the dependent variable, while the independent variables are those which have previously been identified as having an effect on demand. If, for example, the firm had decided that the only variables affecting demand for a particular product with its own price and advertising levels then the linear demand function would be written as:
Q = a + bP + cA
Alternatively, under these conditions the exponential (power) function would be
written as:
Q = a P b A c

In each case, the a term represents the intercept of the-line drawn from the equation with the vertical axis. The b and c terms represent the regression coefficients with respect to own price and advertising respectively. These show the
impact of each of these variables on product demand. Once they have been estimated it is possible to predict the level of demand for any set of values of the independent variables simply by substituting them into the equation.


The exponential form of the equation has the advantage that it can be rewritten to give direct estimates of the respective elasticities of demand for the independent variables. This is done by taking the log-linear form of the equation which in this case would be:

log Q = log a + b log P + c log A

Where b and c are the own price and advertising elasticities of demand respectively. This is a much easier approach than calculating elasticities through use of the linear form which involves using the equation: ED = b . to calculate the elasticities in each case. In this case values of P and Q need to be obtained from the data set. Usually average values are substituted in the above equation to estimate elasticities. This idea will be explored in greater detail in Block 2.
Which of the two forms of equation is chosen depends upon the expected relationship between the variables being included. In practice, however, the actual relationship between them may not be known in advance. In this case, the decision maker may experiment with both forms of equation in order to find the one which most closely fits the data.


ESTIMATING THE REGRESSION EQUATION

Consider a firm with a fixed capital stock that has been rented under a long-term lease for Rs. 100 per production period. The other input in the firm’s production process is labour, which can be increased or decreased quickly depending on the
firm’s needs. In this case, the cost of the capital input (Rs.100) is fixed and the cost of labour is variable. The manager of the firm wants to know the relationship between output and cost, that is, the firm’s total cost function. This would allow the manager to predict the cost of any specified rate of output for the next production period.

Specifically, the manager is interested in estimating the coefficients a and b of the function
Y = a + bX

where the dependent variable Y is total cost and the independent variable X is total output. If this function is plotted on a graph, the parameter a would be the vertical intercept (i.e., the point where the function intersects the vertical axis) and b would be the slope of the function. Recall that the slope of a total function is the marginal function. As Y = a + bX is the total cost function, the slope, b, is marginal cost or the change in total cost per unit change in output.

Assume that data on cost and output have been collected for each of seven production periods and are reported in production periods and are reported in below table. Note that there is a cost of Rs. 100 associated with an output rate of zero. This represents the fixed cost of the capital input, which must be paid regardless of the rate of output. These data are shown as points above Figure . They suggest a definite upward trend, but they do not trace out a straight line. The problem is to determine the line that best represents the overall relationship between Y and X. One approach would simply
be to “eyeball” a line through these data in a way that the data points were about equally spaced on both sides of the line. The coefficient a would be found by extending that line to the vertical axis and reading the Y-coordinate at that point.
The slope, b, would be found by taking any two points on the line, {X1, Y1} and {X2, Y2} and using the slope formula

= (y2−y1)/(x2-x1)

Although this approach could be used, the method is quite imprecise and can be employed only when there is just one independent variable. What if production cost depends on both the rate of output and the size of the plant? To plot the data for these three variables (total cost, output, and plant size) would require a threedimensional diagram; it would be nearly impossible to eyeball the relationship in this case. The addition of another independent variable, say average skill levels of the employees, would place the data set in the fourth dimension, where any graphic approach is hopeless.

There is a better way. Statisticians have demonstrated that the best estimate of the coefficients of a linear function is to fit the line through the data points so that the sum of squared vertical distances from each point to the line is minimized. This technique is called ordinary least-squares regression (OLS) estimation and a number of statistical packages, including excel. Based on the output and cost data , the least-squares regression equation will be shown to be
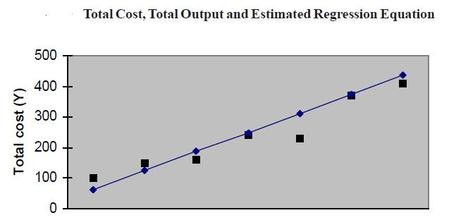
Yˆ = 87.08 + 12.21X This equation is plotted in  below Figure . Note that the data points fall about equally on both sides of the line. Consider an output rate of 5. As shown in above table , the actual cost associated with this output level is 150.

The value predicted by theregression equation, referred to as Yˆ, is 148.13. That is, Yˆ = 87.08 + 12.21(5)=148.13. The deviation of the actual Y value from the predicted value (i.e., the Introduction to ManagerialEconomics14vertical distance of the point from the line), Yˆ i – Yˆ is referred to as the residual or the prediction error.

There are many values that might be selected as estimators of a and b, but only one of those sets defines a line that minimizes the sum of squared deviations [i.e., that minimizes q(Yi -Yi)2]. The equations for computing the least-squares estimators and bˆ are
=
and
â = Y – bˆx_
where Y and - bˆx_ are the means of the Y and X variables. Using the basic cost and output data from the example, the necessary calculations are shown in table 3.3. Substituting the appropriate values into the following equations, the estimates â of bˆ and are computed to be

The estimate of the coefficient a is 87.08. This is the vertical intercept of the regression line. In the context of this example, â = 87.08 is an estimate of fixed cost. Note that this estimate is subject to error because it is known that the actual fixed cost is Rs.100. The value of bˆ is an estimate of the change in total cost for a one-unit change in output (i.e., marginal cost). The value of bˆ , Rs. 12.21, means that, on an average, a one-unit change in output results in Rs. 12.21 change in total cost. Thus bˆ is an estimate of marginal cost.

DECISION UNDER RISK

The focus of this section is decision making under risk. The objective will be to develop guidelines for making rational decisions given the decision makers attitudes towards risk Attitudes towards risk may be of three types:
(a) A risk-seeker is one who prefers risk, given a choice between more or less risky investments, with identical expected money returns; he will select the riskier investment.
(b) A riskaverter is one who faced with the same situation will select the less risky investment.
(c) A risk-neutral person is one who faced with the same situation will be indifferent to the choice. For him any investment is equally preferable to the other.

It is difficult to slot people in one of these categories. You would perhaps have observed both risk averse and risk seeking behaviour in the real world. The analysis of risk is based largely on the concepts of probability and probability distribution that are commonly encountered in elementary statistics. First the terms strategy, states of nature and outcomes need to be defined. A strategy is one of the many alternative plans or courses of action that could be implemented in order to
achieve managerial goal. A manager might be considering three strategies to increase profits - build a more modern plant which may produce at low cost, implement a new marketing programme to increase sales or change the design of
product to decrease cost and increase sales.

A state of nature is a condition that may exist in the future and that will have a significant effect on the success of a strategy. For example, the manager may not be aware of the economic conditions in the future. The possible states of nature may be normal, recession or boom.

The outcome results in either gain or loss based on a particular combination of strategy and state of nature. The decision maker has no control over the states of nature that will prevail in future but the future states of nature will certainly affect the outcome of any strategy that he or she may adopt. The particular decision made will depend, therefore, on the decision maker’s knowledge or estimation of how a particular future state of nature will affect the outcome of each particular strategy. Given a set of outcomes, Xi, and the probability of each occurring, Pi, three statistics relating to probability distributions can be used

These statistics have a direct application in measuring the expected return and risk associated with any business decision for which a set of outcomes and their
probabilities have been determined. The expected value, standard deviation, and the coefficient will be referred to as risk-return evaluation statistics. Having defined risk and reviewed some of the related terminology, the task now is
to develop quantitative measures of return and risk and to show how they are applied in decision making. We know that individuals have different preferences concerning risk taking. It is also important that such preferences be identified and
their effect on decisions evaluated. Rational decision making requires that the expected return be determined and the risk be measured, and that there be information about the manager’s preference for risk. The expected value, the
standard deviation, and the coefficient of variation will be referred to as risk-return evaluation statistics.

Let us take an example where two investments, I and II, are being considered. Both investments require an initial cash outlay of Rs.100 and have a life of five years. The return on each depends on the rate of inflation over the five-year period.

Of course, the inflation rate is not known with certainty, but suppose that the collective judgment of economists is that the probability of no inflation is 0.20, the probability of moderate inflation is 0.50, and the probability of rapid inflation is 0.30.

The outcomes are defined as the present value of net profits for the next five years. These outcomes for each state of nature (i.e., rate of inflation) for each investment are shown in table 3.3. Analysis of these investments can be made by calculating and comparing the three evaluation statistics for each alternative. The expected value μ is an estimate of the
expected return for the investment. Because risk has been defined in terms of the variability in outcomes, the standard deviation s is a measure of risk associated with the investment. The larger the m the greater is the risk. Risk per rupee of expected return is measured by the coefficient of variation (y).

The evaluation statistics for each investment alternative are computed as follows:

Decision Tree
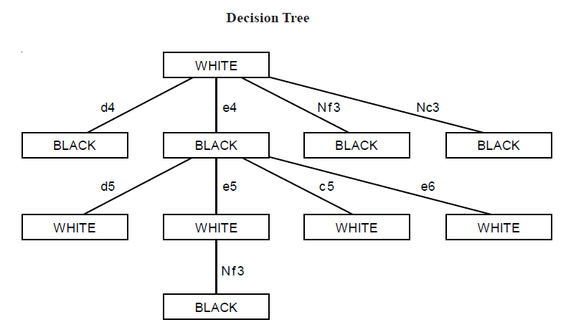
Some strategic decisions are based on a sequence of decisions, states of nature and possibly even strategic decisions. Alternative strategies can be evaluated then, by using a decision tree, which traces sequences of strategies and states of nature to arrive at a set of outcomes. The probability of each outcome is found by multiplying the probabilities on each branch leading to that outcome.A decision tree shows two or more branches at each point where a decision or event (state of nature) leads to the various outcomes. The decision tree approach can be directly applied to managerial decision-making. A firm entering a new market may decide to build a small or large plant (managerial decisions). This has
no probabilities. But there may be stochastic elements (an outcome determined by chance) associated with each decision

e.g., reaction of a major competitor and the economic condition. The competitor may react by starting a national, regional, or a new advertising program. The probability of each occurrence will depend on the size of the plant.

The possible economic conditions and then probabilities may be recession, normal or boom. Here also the probability will depend on the size of the plant. The probability of each combination is found by multiplying the probability along each of
the branches leading to the outcome. For example, if the manager decides to build a large plant there is a 70 per cent chance that the competitor will respond with a national advertisement. We are given that there is a 30 per cent chance of a boom. The probability associated with the outcome of 80 is therefore 0.21 (=0.7*0.3). Similar for other entries in the decision tree. Decision trees are particularly useful if sequential decision-making is involved. In a game of chess, white has the first move. White has several options at this stage. To keep the problem tractable, let us assume that there are four possible moves for white :
(i) move the king’s pawn two squares;
(ii) move the queen’s pawn two squares;
(iii) move the king’s knight to king bishop three; and
(iv) move the queen’s knight to queen bishop three.

In chess notation, the four moves are - (i) e4; (ii) d4;(iii) Nf 3; and (iv) Nc 3. Once white has made the first move, Black has several different moves at his disposal. To keep the problem tractable, let us follow the decision tree only when white has moved e4. Even then, Black has several moves at his disposal. Let us assume that he has only four options - (i) move the king’s pawn two squares (e5), (ii) move the queen’s pawn two squares (d5); (iii) move the queen’s bishop’s pawn two squares (c5); and (iv) move the king’s pawn one square (e6). Once white has moved e4 on the first move and Black has moved e5 on the first move, white has several moves at his disposal. One of them is, move the king’s
knight to bishop three (Nf3). And so the game goes on.

Each vertex or node indicates a decision to be taken by one of the players, the number within the rectangle indicating whose turn it is to move. There need not actually be two players, one of the players can be regarded as nature or chance.
The main advantage of using a decision tree is that it helps one to isolate each chain and follow it through to the very end.

UNCERTAINITY ANALYSIS AND DECISION MAKING

Certainty appears to be a theoretical and impractical state, as here the investor has perfect knowledge of the investment environment such that he is definite about the size, regularity and periodicity of flow of returns. Such situations may exist in the short-run (e.g. fixed deposit in a nationalised bank). However, long-run or longrange investments are not predictable as they are influenced by many kinds of changes taking place with time: political, economic, market and technology etc. Risk is more common in the real world. A situation with more than one possible outcome to a decision such that the probability of each of these outcomes can be measured is a risk situation. For example, tossing of a coin (i.e. 50-50) or investing in a stock. The greater the number and range of outcomes, the greater is the risk associated with the decision or action. Uncertainty is a situation where there is more than one possible outcome to a decision but the probability of each specific outcome occurring is not known or even meaningful. This may be due to insufficient information or instability in the nature of variables. In extremes cases of uncertainty, the outcomes may itself be not clear. Decision making under uncertainty is necessarily subjective.

The Risk Faced by Coca Cola in changing its secret formula.
On April 23, 1985, the Coca Cola Company announced that it was changing its 99-year old recipe for Coke. Coke is the leading soft drink in the world, the company took an unusual risk in tempering its highly successful product. The Coca Cola
Company felt that changing its recipe was a necessary strategy to ward off the challenge from Pepsi - Cola, which had been chipping away at Coke’s market over the years. The new Coke, with its sweeter less fizzy taste, was clearly aimed at reversing Pepsi’s market gains. Coca Cola spent over $. 4 million to develop its new Coke and conducted taste tests on more than 1,90,000 consumers over a three-year period. These seemed to indicate that consumers preferred the new
Coke by 61 percent i.e. 39 percent over the old Coca Cola - Cola then spent over $ 10 million on advertising its new product.

When the new Coke was finally introduced in May 1985, there was nothing short of a consumers’ revolt against the new Coke, and in what is certainly one of the most stunning multimillion dollar about faces in the history of marketing, the
company felt compelled to bring back the old Coke under the brand name of Coca Cola Classic. The irony is that with the Classic and new Cokes sold side by side, Coca Cola regained some of the market share that it had lost to Pepsi. While some people believe that Coca-Cola intended all along to reintroduce the old Coke and that the whole thing was part of a shrewd marketing strategy, yet most marketing experts are convinced that Coca Cola had underestimated consumers’ loyalty to the old Coke. This did not come up in the extensive taste-tests conducted by Coca-Cola because the consumers tested were newer informed that the company intended to “replace” the old Coke with the new Cola, rather than sell them side by side. This case clearly shows that even a well conceived strategy is risky and can lead to results estimated to have a small probability of occurrence. Indeed, the failure rate for new products in the United States is a stunning 80 percent

ROLE OF MANAGERIAL ECONOMIST
In general, managerial economics can be used by the goal-oriented manager in two ways. First, given an existing economic environment, the principles of managerial economics provide a framework for evaluating whether resources are being allocated efficiently within a firm. For example, economics can help the manager if profit could be increased by reallocating labour from a marketing activity to the production line. Second, these principles help the manager to respond to various economic signals. For example, given an increase in the price of output or the development of a new lower-cost production technology, the appropriate managerial response would be to increase output. Alternatively, an increase in the
price of one input, say labour, may be a signal to substitute other inputs, such as capital, for labour in the production process. Thus, the working knowledge of the principles of managerial economics can increase the value of both the firm and the manager.


SUMMARY
Various quantitative tools are used by the manager to help him in making decisions. An opportunity set is a set of alternative actions which are feasible. Variables are things which can change and can take a set of possible values within a given problem. A function shows the relation between two variables. It can take different forms-linear, quadratic, cubic. Partial derivatives are functions of all variables entering into the original function f(x). Optimisation is the act of choosing the best alternative out of all available ones. Regression analysis helps to determine values of the parameters of a function - Economic analysis of risk becomes crucial with reference to decisions.