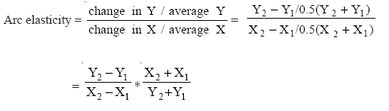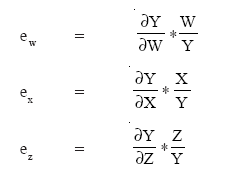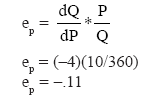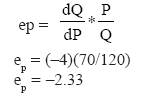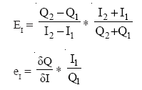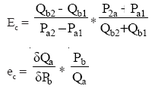INTRODUCTION
In the previous unit, we studied that when price falls, quantity demanded would increase. While we know this qualitative effect exists for most goods and services, managers and business analysts are often more interested in knowing the magnitude of the response to a price change i.e. by how much? There are many situations in which one might want to measure how sensitive the quantity demanded is to changes in a product’s price. Economists and other business analysts are frequently concerned with the responsiveness of one variable to changes in some other variable. It is useful to know, for example, what effect a given percentage change in price would have on sales. The most widely adopted measure of responsiveness is elasticity. Elasticity is a general concept that economists, business people, and government officials rely on for such measurement. For example, the finance minister might be interested in knowing whether decreasing tax rates would increase tax revenue. Likewise, it is often useful to measure the sensitivity of changes in demand to changes in one of the determinants of demand,such as income or advertising. Elasticity is defined as the ratio of the percentage change in quantity demanded to the percentage change in some factor (such as price or income) that stimulates the change in quantity. The reason for using percentage change is that it obviates the need to know the units in which quantity and price are measured. For example quantity could be in kilograms, grams, litres or gallons and price could be in dollars, rupees, euro etc. A measure of elasticity based on units would lead to confusion and misleading comparisons across different products. The use of percentage change makes the measure of elasticity independent of units of measurement and
hence easy to understand.Elasticity is the percentage change in some dependent variable given a one-percent change in an independent variable, ceteris paribus. If we let Y represent the dependent variable, X the independent variable, and E the elasticity, then elasticity is represented as E = % change in Y / % change in X There are two forms of elasticity: arc elasticity and point elasticity. The former reflects the average responsiveness of the dependent variable to changes in the independent variable over some interval. The numeric value of arc elasticity can befound as follows:
In the previous unit, we studied that when price falls, quantity demanded would increase. While we know this qualitative effect exists for most goods and services, managers and business analysts are often more interested in knowing the magnitude of the response to a price change i.e. by how much? There are many situations in which one might want to measure how sensitive the quantity demanded is to changes in a product’s price. Economists and other business analysts are frequently concerned with the responsiveness of one variable to changes in some other variable. It is useful to know, for example, what effect a given percentage change in price would have on sales. The most widely adopted measure of responsiveness is elasticity. Elasticity is a general concept that economists, business people, and government officials rely on for such measurement. For example, the finance minister might be interested in knowing whether decreasing tax rates would increase tax revenue. Likewise, it is often useful to measure the sensitivity of changes in demand to changes in one of the determinants of demand,such as income or advertising. Elasticity is defined as the ratio of the percentage change in quantity demanded to the percentage change in some factor (such as price or income) that stimulates the change in quantity. The reason for using percentage change is that it obviates the need to know the units in which quantity and price are measured. For example quantity could be in kilograms, grams, litres or gallons and price could be in dollars, rupees, euro etc. A measure of elasticity based on units would lead to confusion and misleading comparisons across different products. The use of percentage change makes the measure of elasticity independent of units of measurement and
hence easy to understand.Elasticity is the percentage change in some dependent variable given a one-percent change in an independent variable, ceteris paribus. If we let Y represent the dependent variable, X the independent variable, and E the elasticity, then elasticity is represented as E = % change in Y / % change in X There are two forms of elasticity: arc elasticity and point elasticity. The former reflects the average responsiveness of the dependent variable to changes in the independent variable over some interval. The numeric value of arc elasticity can befound as follows:
where the subscripts refer to the two data points observed, or the extremes of the interval for which the elasticity is calculated.
Point elasticities indicate the responsiveness of the dependent variable to the independent variable at one particular point on the demand curve. Point elasticities are calculated as follows: (e) = δX/δY*1X/1Y This form works well when the function is bivariate: Y = f (X). However, when there are more independent variables, partial derivatives must be used. For example, suppose that Y = f(W,X,Z) and we want to find the elasticities for each ofthe independent variables. We would have
Point elasticities indicate the responsiveness of the dependent variable to the independent variable at one particular point on the demand curve. Point elasticities are calculated as follows: (e) = δX/δY*1X/1Y This form works well when the function is bivariate: Y = f (X). However, when there are more independent variables, partial derivatives must be used. For example, suppose that Y = f(W,X,Z) and we want to find the elasticities for each ofthe independent variables. We would have
Although economists use a great variety of elasticities, the following three deserve particular attention because of their wide application in the business world: price elasticity, income elasticity, and cross-price elasticity. We discuss these in detail in the subsequent sections.
THE PRICE ELASTICITY OF DEMAND
Price elasticity of demand measures the responsiveness of the quantity sold to changes in the product’s price, ceteris paribus. It is the percentage change in sales divided by a percentage change in price. The notation Ep will be used for the are price elasticity of demand, and ep will be used for the point price elasticity of demand. If the absolute value of Ep (or ep ) is greater than one, a given percentage decrease (increase) in price will result in an even greater percentage increase (decrease) in sales.1 In such a case, the demand for the product is considered elastic; that is, sales are relatively responsive to price changes. Therefore, the percentage change in quantity demanded will be greater than the percentage change in the price. When the absolute value of the price elasticity of demand is less than one, the percentage change in sales is less than a given percentage change in price. Demand is then said to be inelastic with respect to price. Unitary price elasticity results when a given percentage change in price results in an equal percentage change in sales. The absolute value of the coefficient of price elasticity is equal to one in such cases. These relationships are summarized as follows:
If |ep| or |Ep |> 1, demand is elastic
If |ep| or |Ep| < 1, demand is inelasticIf |ep| or |Ep| = 1, demand is unitarily elastic
ARC PRICE ELASTICITY
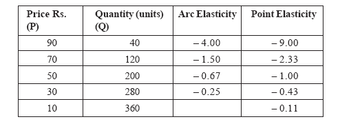
Consider the hypothetical prices of some product and the corresponding quantity demanded, as given in Table 5.1. We could calculate the arc price elasticity between the two lowest prices i.e. between Rs. 30 and Rs. 10 as follows:Ep = (360- 280)/(360+ 280)/(10- 30)/ (10+ 30)=2.5
Thus, demand is inelastic in this range. This value of Ep = – .25 means that a one
percent change in price results in a .25% change in the quantity demanded (in theopposite direction of the price change) over this region of the demand function.
THE PRICE ELASTICITY OF DEMAND
Price elasticity of demand measures the responsiveness of the quantity sold to changes in the product’s price, ceteris paribus. It is the percentage change in sales divided by a percentage change in price. The notation Ep will be used for the are price elasticity of demand, and ep will be used for the point price elasticity of demand. If the absolute value of Ep (or ep ) is greater than one, a given percentage decrease (increase) in price will result in an even greater percentage increase (decrease) in sales.1 In such a case, the demand for the product is considered elastic; that is, sales are relatively responsive to price changes. Therefore, the percentage change in quantity demanded will be greater than the percentage change in the price. When the absolute value of the price elasticity of demand is less than one, the percentage change in sales is less than a given percentage change in price. Demand is then said to be inelastic with respect to price. Unitary price elasticity results when a given percentage change in price results in an equal percentage change in sales. The absolute value of the coefficient of price elasticity is equal to one in such cases. These relationships are summarized as follows:
If |ep| or |Ep |> 1, demand is elastic
If |ep| or |Ep| < 1, demand is inelasticIf |ep| or |Ep| = 1, demand is unitarily elastic
ARC PRICE ELASTICITY
Consider the hypothetical prices of some product and the corresponding quantity demanded, as given in Table 5.1. We could calculate the arc price elasticity between the two lowest prices i.e. between Rs. 30 and Rs. 10 as follows:Ep = (360- 280)/(360+ 280)/(10- 30)/ (10+ 30)=2.5
Thus, demand is inelastic in this range. This value of Ep = – .25 means that a one
percent change in price results in a .25% change in the quantity demanded (in theopposite direction of the price change) over this region of the demand function.
If we calculate the arc price elasticity between the prices of 50 and 70, we have
Ep= (200 -120)/(200 +120) /(50 -70)/ (50 +70) = 1.5 We would say that demand is price elastic in this range because the percentage change in sales is greater than the percentage change in price. You can calculate arc elasticity over any price range. As an exercise estimate the arc elasticity between the extremes of the demand function shown in Table , i.e. between Rs. 90 and Rs. 10. Satisfy yourself that the absolute value of arc elasticity between
these two points is 1.
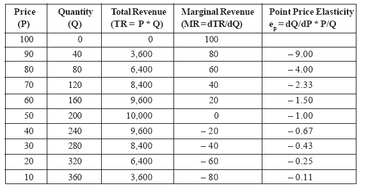
POINT PRICE ELASTICITY
The algebraic equation for the demand schedule given in Table is P = 100 – .25Q or Q = 400 – 4P We can use this demand function to illustrate the determination of point price elasticities. Let’s select the point at which P = 10 and Q = 360:
Because |ep| < 1, we would say that demand is inelastic at a price of Rs. 10. Now,consider a price of Rs. 70:
Here, |ep| > 1, and demand is price elastic. This example shows that the price elasticity of demand may (and usually does) vary along any demand function, depending on the portion of the function for which the elasticity is calculated. It follows that we usually cannot make such statements as "the demand for product X is elastic" because it is likely to be elastic for one range of prices and inelastic for another. Usually at high prices demand is elastic,
while at lower prices demand tends to be inelastic. Intuitively, this is so because lowering price from very high levels is likely to stimulate demand much more compared to lowering prices when price is already low. As an illustration, consider the prices of cellular phones (handsets) when these were first introduced in the Indian market at prices ranging between Rs. 25,000 to Rs. 30,000 per handset. Demand was limited to the higher end of the market. As these prices fell, demand was stimulated and resulted in increasing penetration in the middle and lower end segments, indicating an elastic response.
PRICE ELASTICITY AND REVENUE
We have defined demand to be elastic when the absolute value of the price elasticity is greater than one. For that to be true, the percentage change in quantity must be greater than the percentage change in price (% change in Q > % change in P). If this were true, what would you expect to happen to a firm’s receipts if the price were lowered? Recall from principles of economics that total revenue (TR) is equal to price (P) times quantity (Q). Consider an extreme case. Suppose that a five-percent cut in price stimulates a fifty-per cent increase in sales (the price elasticity would be 10). You would expect
revenues to rise. The relatively small drop in price would be more than compensated for by a large increase in sales. To see exactly the relationship between total revenue and price elasticity, let’s return to the demand function given by the equation Q = 400 – 4P which is used as the basis for Table 5.2. The tableshows how the price elasticity of demand varies along the demand curve.
while at lower prices demand tends to be inelastic. Intuitively, this is so because lowering price from very high levels is likely to stimulate demand much more compared to lowering prices when price is already low. As an illustration, consider the prices of cellular phones (handsets) when these were first introduced in the Indian market at prices ranging between Rs. 25,000 to Rs. 30,000 per handset. Demand was limited to the higher end of the market. As these prices fell, demand was stimulated and resulted in increasing penetration in the middle and lower end segments, indicating an elastic response.
PRICE ELASTICITY AND REVENUE
We have defined demand to be elastic when the absolute value of the price elasticity is greater than one. For that to be true, the percentage change in quantity must be greater than the percentage change in price (% change in Q > % change in P). If this were true, what would you expect to happen to a firm’s receipts if the price were lowered? Recall from principles of economics that total revenue (TR) is equal to price (P) times quantity (Q). Consider an extreme case. Suppose that a five-percent cut in price stimulates a fifty-per cent increase in sales (the price elasticity would be 10). You would expect
revenues to rise. The relatively small drop in price would be more than compensated for by a large increase in sales. To see exactly the relationship between total revenue and price elasticity, let’s return to the demand function given by the equation Q = 400 – 4P which is used as the basis for Table 5.2. The tableshows how the price elasticity of demand varies along the demand curve.
Note that no point elasticity can be calculated when Q = 0 because division by zero is not defined. In this table, total revenue and marginal revenue are included, as well as the point price elasticities. Marginal revenue (MR) is defined as the rate of change in total revenue, or the additional revenue generated by selling one more unit. In this example, the demand function can be solved for P in terms of Q as follows
Consider Q = 400 – 4P
Þ 4P = 400 – Q
Þ P = 100 – 0.25Q
Multiplying by Q and taking the first derivative yields:
TR = P.Q
TR = (100 – .25Q)Q
TR = 100Q – 0.25Q2
MR = dTR/dQ
MR = 100 – 0.5Q
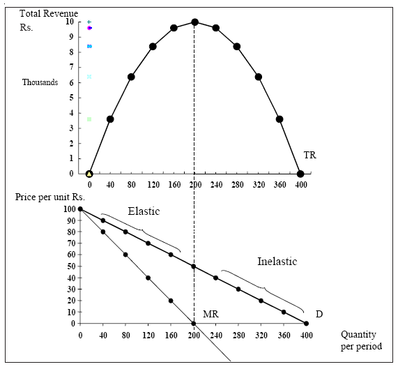
The total revenue and marginal revenue functions along with the demand curve, are plotted in Figure . Notice that the slope of the marginal revenue function is twice the slope of the demand function. You see in Figure that demand is price elastic over the range of quantities for which marginal revenue is positive. Because marginal revenue is the slope of total revenue (remember that MR = dTR/dQ), you can tell that increasing sales by lowering price will cause total revenue to rise over this interval. However, lowering price when demand is inelastic (beyond Q = 200) will result in reduced revenues. From an examination of Figure and Table, we can reach some important conclusions about the relationship between elasticity and total revenue. As is evident from the above discussion, the change in expenditure when price changes is related to the elasticity of demand. If elasticity is less than unity (inelastic), the percentage change in price can exceed the percentage change in
Consider Q = 400 – 4P
Þ 4P = 400 – Q
Þ P = 100 – 0.25Q
Multiplying by Q and taking the first derivative yields:
TR = P.Q
TR = (100 – .25Q)Q
TR = 100Q – 0.25Q2
MR = dTR/dQ
MR = 100 – 0.5Q
The total revenue and marginal revenue functions along with the demand curve, are plotted in Figure . Notice that the slope of the marginal revenue function is twice the slope of the demand function. You see in Figure that demand is price elastic over the range of quantities for which marginal revenue is positive. Because marginal revenue is the slope of total revenue (remember that MR = dTR/dQ), you can tell that increasing sales by lowering price will cause total revenue to rise over this interval. However, lowering price when demand is inelastic (beyond Q = 200) will result in reduced revenues. From an examination of Figure and Table, we can reach some important conclusions about the relationship between elasticity and total revenue. As is evident from the above discussion, the change in expenditure when price changes is related to the elasticity of demand. If elasticity is less than unity (inelastic), the percentage change in price can exceed the percentage change in
quantity. The price change will then be the dominant one of the two changes and the revenue will change in the same direction as the price change. If however,elasticity exceeds unity (elastic), the percentage change in quantity will exceed the percentage change in price. The percentage change in quantity will be the more important change, so that total expenditure will change in the opposite direction as the price change. These results can be summarized as follows:
Elastic Demand
1. Decrease price....... Increase total revenue
2. Increase price.........Decrease total revenue
Price and total revenue move in opposite directions.
Inelastic Demand
1. Decrease price....... Decrease total revenue
2. Increase price.........Increase total revenue
Price and total revenue move in the same direction.If a demand function has a unitary elasticity, then the same level of revenue will be generated, regardless of price. You see that for a linear demand function, as price falls, demand becomes less elastic or more inelastic. You have also seen that when
demand is elastic, price cuts are associated with increases in total revenue. But if price continues to be lowered in the range in which demand is inelastic, total revenue will fall. Thus, total revenue will be maximized at the price (and related quantity) at which demand is unitarily elastic. You can see from Figure that this point is also where MR = 0. This observation makes sense because marginal revenue is the slope of total revenue. Recall that any function may have a maximum where its slope is zero. For total revenue, we have
TR = P.Q = (100 – 0.25Q) Q
TR = 100Q – 0.25Q2
dTR/dQ = 100 – 0.5Q
Setting the first derivative equal to 0 and solving for Q, we find
dTR/dQ = 100 – .5Q = 0
–.50Q = –100
Q = 200
Checking the second-order condition, we see that
d2TR/dQ2 = – 0.5 < 0
Because the second derivative is negative, we know that total revenue is a maximum at Q = 200. The price at which 200 units will sell is Rs. 50, so that is the revenue-maximizing price.The relationship between elasticity and total revenue can also be shown using calculus. Total revenue is price times quantity. Taking the derivative of total revenue with respect to quantity yields marginal revenue:TR = P.Q = (100 – 0.25Q) Q
TR = 100Q – 0.25Q2dTR/dQ = 100 – 0.5Q The equation states that the additional revenue resulting from the sale of one more unit of a good or service is equal to the selling price of the last unit (P), adjusted for the reduced revenue from all other units sold at a lower price (QdP/dQ). This equation can be written MR = P (1+ PdQ/QdP) But note that (Q/P) dP/dQ = l / ep. Thus MR = P (1+ ) This equation indicates that marginal revenue is a function of the elasticity of demand. For example, if demand is unitary elastic, ep = –1 then2 MR = P ( l + 1/−1 ) = 0 Because marginal revenue is zero, a price change would have no effect on total revenue. In contrast, if demand is elastic, say eP = –2, marginal revenue will be greater than zero. This implies that a price reduction, by stimulating a considerable increase in demand would increase total revenue. This equation also implies that if demand is inelastic, say eP = – 0.5, marginal revenue is negative, indicating that a price reduction would decrease total revenue. Some analysts question the usefulness of elasticity estimates. They argue that elasticities are redundant, such that the data necessary for their determination could be used to determine total revenues directly. Thus managers could assess the effects of a change in price without knowledge of price elasticity. Although this is true, elasticity estimates are valuable to the extent that they provide a quick way of evaluating pricing policies. For example, if demand is known to be elastic, it is also known that a price increase will reduce total revenues. Likewise, if the Finance Minister wants to raise revenue through taxation he knows that increasing duties on
cigarettes will most likely generate the result he desires.The next section illustrates the usefulness of knowledge of elasticity.
Illustration
Texas Calculates Elasticity
In addition to its regular license plates, the state of Texas, as do other states, sells personalized or “vanity” license plates. To raise additional revenue, the state will sell a vehicle owner a license plate saying whatever the owner wants as long as it uses six letters (or numbers), no one else has the same license as the one requested, and it isn’t obscene. For this service, the state charges a higher price than the price for standard licenses. Many people are willing to pay the higher price rather than display a license of the standard form such as 387 BRC. For example, an ophthalmologist announces his practice with the license MYOPIA. Others tell their personalities with COZY-1 and ALL MAN. A rabid Star Trek fan has BM ME UP. In 1986, Texas increased the price for such plates from $25 to $75. The Houston Post (October 19, 1986) reported that before the price increase about 150,000 cars in Texas had personalized licenses. After the increase in price, only 60,000 people ordered the vanity plates. As it turned out, demand was rather inelastic over this range. As you can calculate, the own-price elasticity is – 0.86. Thus revenue rose after the price increase, from $3,750,000 to $4,500,000. But the Houston Post article quoted the assistant director of the Texas Division of Motor Vehicles as saying, “Since the demand dropped3 the state didn’t make
money from the higher fees, so the price for next year’s personalized plates will be $40.” If the objective of the state is to make money from these licenses and if the numbers in the article are correct, this is the wrong thing to do. It’s hard to see how the state lost money by increasing the price from $25 to $75—the revenue increased and the cost producing plates must have decreased since fewer were produced. So the move from $25 to $75 was the right move.Moreover, let’s suppose that the elasticity between $75 and $440 is essentially the same as that calculated for the movement from $25 to $475 (–0.86). We can use this estimate to calculate what happens to revenue if the state drops the price to $40. We must first find what the new quantity demanded will be at $40. Using the arc elasticity formula and the elasticity of –0.86.Where Q is the new quantity demanded. Solving this equation for Q, the estimated sales are 102,000 (rounded) at a price of $40. With this quantity demanded and price,total revenue would be $4,080,000 at $75 a plate. If the state’s objective is to raise revenue by selling vanity plates, it should increase rather than decrease price.This application actually makes two points. First, even decision makers in organisations that are not run for profit, such as government agencies, should be able to use economic analysis. Second, managers whose firms are in business to make a profit should make an effort to know (or at least have a good approximation for) the elasticity of demand for the products they sell. Only with this information will they know what price to charge.DETERMINANTS OF PRICE ELASTICITY
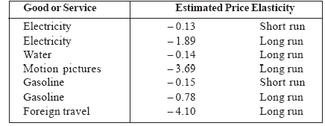
Price elasticities can be estimated for many goods and services; Table 5.3 providessome examples. The short-run elasticities reflect periods of time that are not longenough for the consumer to adjust completely to changes in prices. The long-runvalues refer to situations where consumers have had more time to adjust. Note thevariation in elasticities in Table 5.3. The long-run demand for foreign travel by U.S.residents is elastic (i.e., ep = |4.10|). In contrast, the long-run demand for water ishighly inelastic (i.e., ep = |0.14|). Demand for is inelastic in the short run, but elasticin the long run. In general, three factors determine the price elasticity of demand.They are: (1) availability of substitutes, (2) proportion of income spent on good orservice, and (3) length of time.Availability of Substitutes: The main determinant of elasticity is the availability ofsubstitutes. Products for which there are good substitutes tend to have higher price elasticity of demand than products for which there are few adequate substitutes.Movies are a good example. Movies are a form of recreation, but there are manyalternative recreational activities. When ticket prices at the movie theatre increase,these substitute activities replace movies. Thus, the demand for motion pictures isrelatively elastic, as shown in Table 5.3. Other examples of products with closesubstitutes and therefore elastic demand would be demand for Maruti cars,subscription to cellular services, demand for air-travel etc.
Elastic Demand
1. Decrease price....... Increase total revenue
2. Increase price.........Decrease total revenue
Price and total revenue move in opposite directions.
Inelastic Demand
1. Decrease price....... Decrease total revenue
2. Increase price.........Increase total revenue
Price and total revenue move in the same direction.If a demand function has a unitary elasticity, then the same level of revenue will be generated, regardless of price. You see that for a linear demand function, as price falls, demand becomes less elastic or more inelastic. You have also seen that when
demand is elastic, price cuts are associated with increases in total revenue. But if price continues to be lowered in the range in which demand is inelastic, total revenue will fall. Thus, total revenue will be maximized at the price (and related quantity) at which demand is unitarily elastic. You can see from Figure that this point is also where MR = 0. This observation makes sense because marginal revenue is the slope of total revenue. Recall that any function may have a maximum where its slope is zero. For total revenue, we have
TR = P.Q = (100 – 0.25Q) Q
TR = 100Q – 0.25Q2
dTR/dQ = 100 – 0.5Q
Setting the first derivative equal to 0 and solving for Q, we find
dTR/dQ = 100 – .5Q = 0
–.50Q = –100
Q = 200
Checking the second-order condition, we see that
d2TR/dQ2 = – 0.5 < 0
Because the second derivative is negative, we know that total revenue is a maximum at Q = 200. The price at which 200 units will sell is Rs. 50, so that is the revenue-maximizing price.The relationship between elasticity and total revenue can also be shown using calculus. Total revenue is price times quantity. Taking the derivative of total revenue with respect to quantity yields marginal revenue:TR = P.Q = (100 – 0.25Q) Q
TR = 100Q – 0.25Q2dTR/dQ = 100 – 0.5Q The equation states that the additional revenue resulting from the sale of one more unit of a good or service is equal to the selling price of the last unit (P), adjusted for the reduced revenue from all other units sold at a lower price (QdP/dQ). This equation can be written MR = P (1+ PdQ/QdP) But note that (Q/P) dP/dQ = l / ep. Thus MR = P (1+ ) This equation indicates that marginal revenue is a function of the elasticity of demand. For example, if demand is unitary elastic, ep = –1 then2 MR = P ( l + 1/−1 ) = 0 Because marginal revenue is zero, a price change would have no effect on total revenue. In contrast, if demand is elastic, say eP = –2, marginal revenue will be greater than zero. This implies that a price reduction, by stimulating a considerable increase in demand would increase total revenue. This equation also implies that if demand is inelastic, say eP = – 0.5, marginal revenue is negative, indicating that a price reduction would decrease total revenue. Some analysts question the usefulness of elasticity estimates. They argue that elasticities are redundant, such that the data necessary for their determination could be used to determine total revenues directly. Thus managers could assess the effects of a change in price without knowledge of price elasticity. Although this is true, elasticity estimates are valuable to the extent that they provide a quick way of evaluating pricing policies. For example, if demand is known to be elastic, it is also known that a price increase will reduce total revenues. Likewise, if the Finance Minister wants to raise revenue through taxation he knows that increasing duties on
cigarettes will most likely generate the result he desires.The next section illustrates the usefulness of knowledge of elasticity.
Illustration
Texas Calculates Elasticity
In addition to its regular license plates, the state of Texas, as do other states, sells personalized or “vanity” license plates. To raise additional revenue, the state will sell a vehicle owner a license plate saying whatever the owner wants as long as it uses six letters (or numbers), no one else has the same license as the one requested, and it isn’t obscene. For this service, the state charges a higher price than the price for standard licenses. Many people are willing to pay the higher price rather than display a license of the standard form such as 387 BRC. For example, an ophthalmologist announces his practice with the license MYOPIA. Others tell their personalities with COZY-1 and ALL MAN. A rabid Star Trek fan has BM ME UP. In 1986, Texas increased the price for such plates from $25 to $75. The Houston Post (October 19, 1986) reported that before the price increase about 150,000 cars in Texas had personalized licenses. After the increase in price, only 60,000 people ordered the vanity plates. As it turned out, demand was rather inelastic over this range. As you can calculate, the own-price elasticity is – 0.86. Thus revenue rose after the price increase, from $3,750,000 to $4,500,000. But the Houston Post article quoted the assistant director of the Texas Division of Motor Vehicles as saying, “Since the demand dropped3 the state didn’t make
money from the higher fees, so the price for next year’s personalized plates will be $40.” If the objective of the state is to make money from these licenses and if the numbers in the article are correct, this is the wrong thing to do. It’s hard to see how the state lost money by increasing the price from $25 to $75—the revenue increased and the cost producing plates must have decreased since fewer were produced. So the move from $25 to $75 was the right move.Moreover, let’s suppose that the elasticity between $75 and $440 is essentially the same as that calculated for the movement from $25 to $475 (–0.86). We can use this estimate to calculate what happens to revenue if the state drops the price to $40. We must first find what the new quantity demanded will be at $40. Using the arc elasticity formula and the elasticity of –0.86.Where Q is the new quantity demanded. Solving this equation for Q, the estimated sales are 102,000 (rounded) at a price of $40. With this quantity demanded and price,total revenue would be $4,080,000 at $75 a plate. If the state’s objective is to raise revenue by selling vanity plates, it should increase rather than decrease price.This application actually makes two points. First, even decision makers in organisations that are not run for profit, such as government agencies, should be able to use economic analysis. Second, managers whose firms are in business to make a profit should make an effort to know (or at least have a good approximation for) the elasticity of demand for the products they sell. Only with this information will they know what price to charge.DETERMINANTS OF PRICE ELASTICITY
Price elasticities can be estimated for many goods and services; Table 5.3 providessome examples. The short-run elasticities reflect periods of time that are not longenough for the consumer to adjust completely to changes in prices. The long-runvalues refer to situations where consumers have had more time to adjust. Note thevariation in elasticities in Table 5.3. The long-run demand for foreign travel by U.S.residents is elastic (i.e., ep = |4.10|). In contrast, the long-run demand for water ishighly inelastic (i.e., ep = |0.14|). Demand for is inelastic in the short run, but elasticin the long run. In general, three factors determine the price elasticity of demand.They are: (1) availability of substitutes, (2) proportion of income spent on good orservice, and (3) length of time.Availability of Substitutes: The main determinant of elasticity is the availability ofsubstitutes. Products for which there are good substitutes tend to have higher price elasticity of demand than products for which there are few adequate substitutes.Movies are a good example. Movies are a form of recreation, but there are manyalternative recreational activities. When ticket prices at the movie theatre increase,these substitute activities replace movies. Thus, the demand for motion pictures isrelatively elastic, as shown in Table 5.3. Other examples of products with closesubstitutes and therefore elastic demand would be demand for Maruti cars,subscription to cellular services, demand for air-travel etc.
Sources: H. S. Houthakker and L. D. Taylor, Consumer Demand in the United States. Analysis and Projections (Cambridge, Mass.: Harvard University Press, 1970), and I. L. Sweeney, “The Demand for Gasoline: A Vintage Capital Model,”Department of Engineering Economics, Stanford University, 1975.
At the other extreme, consider the short-run demand for electricity. When your local supplier increases prices, consumers have few options. There are not many short-run alternatives to using electricity for cooling and lighting. Hence the shortrun demand for electricity is relatively inelastic. In the days of the license raj in India, when government was the monopoly provider, demand for telecom services was relatively inelastic since there was no other service provider in the market. Thus, a product with close substitutes tends to have elastic demand; one with no close substitutes tends to have inelastic demand. An important mission for most advertising is to make the consumer perceive that no close substitute exists for the product being advertised, thereby rendering the consumers demand relatively inelastic.
Proportion of Income Spent: Demand tends to be inelastic for goods and services that account for only a small proportion of total expenditures. Consider the demand for salt. 250 grams of salt will meet the needs of the typical household for months and costs only a few rupees. If the price of salt were to double, this change would not have a significant impact on the family’s purchasing power. As a result, price changes have little effect on the household demand for salt. In contrast, demand will tend to be more elastic for goods and services that require a substantial portion of total expenditures. Thus demand for holiday travel and luxury cars take up a considerable portion of the family’s budget and therefore tend to have higher elasticities. The relative necessity of a good also influences elasticity. For example, the demand for insulin is probably very inelastic because it is
necessary for diabetics who rely on this drug.Time Period: Demand is usually more elastic in the long run than in the short run. The explanation is that, given more time, the consumer has more opportunities to adjust to changes in prices. Table 5.3 indicates that the long-run elasticity for
electricity is more than ten times the short-run value. Price Elasticity and Decision Making Information about price elasticities can be extremely useful to managers as they contemplate pricing decisions, if demand is inelastic at the current price, a price decrease will result in a decrease in total revenue. Alternatively, reducing the price of a product with elastic demand would cause revenue to increase. The effect on total revenue would be the reverse for a price increase. However, if demand is unitary elastic, price changes will not change total revenues. However, a price reduction is not always the correct strategy when demand is elastic. The decision must also take into account the impact on the firm’s costs and profits. More will be
said about pricing strategy in Block 4. As another example of how knowledge of price elasticity may be useful, let’s
consider the demand for cigarettes. The price elasticity for cigarettes by age groups
has been found to be:
Age Group Price Elasticity
12-17 years – 1.40
20-25 years – 0.89
26-35 years – 0.47
36-74 years – 0.45These elasticities indicate that young smokers are much more responsive to price than are older smokers. This may be in part related to the fraction of income that goes towards the purchase of cigarettes. It may also reflect the degree to which physical/psychological addiction influences consumption. From the perspective of cigarette sellers, these results suggest that if all sellers increased prices proportionately, the total expenditure on cigarettes by adult smokers would increase. (Recall that when demand is inelastic, price and total revenue move in the same direction). Individual brands would be more price elastic than for the entire product class because each brand has other brands that represent potential substitutes;however, for the product class, there may be few good substitutes.
INCOME ELASTICITY OF DEMAND
The income elasticity of demand measures the responsiveness of sales to changesin income, ceteris paribus. It is defined as the percentage change in sales dividedby the corresponding percentage change in income. The methods used to calculatearc income elasticity (EI) and point income elasticity (eI)are as follows:
At the other extreme, consider the short-run demand for electricity. When your local supplier increases prices, consumers have few options. There are not many short-run alternatives to using electricity for cooling and lighting. Hence the shortrun demand for electricity is relatively inelastic. In the days of the license raj in India, when government was the monopoly provider, demand for telecom services was relatively inelastic since there was no other service provider in the market. Thus, a product with close substitutes tends to have elastic demand; one with no close substitutes tends to have inelastic demand. An important mission for most advertising is to make the consumer perceive that no close substitute exists for the product being advertised, thereby rendering the consumers demand relatively inelastic.
Proportion of Income Spent: Demand tends to be inelastic for goods and services that account for only a small proportion of total expenditures. Consider the demand for salt. 250 grams of salt will meet the needs of the typical household for months and costs only a few rupees. If the price of salt were to double, this change would not have a significant impact on the family’s purchasing power. As a result, price changes have little effect on the household demand for salt. In contrast, demand will tend to be more elastic for goods and services that require a substantial portion of total expenditures. Thus demand for holiday travel and luxury cars take up a considerable portion of the family’s budget and therefore tend to have higher elasticities. The relative necessity of a good also influences elasticity. For example, the demand for insulin is probably very inelastic because it is
necessary for diabetics who rely on this drug.Time Period: Demand is usually more elastic in the long run than in the short run. The explanation is that, given more time, the consumer has more opportunities to adjust to changes in prices. Table 5.3 indicates that the long-run elasticity for
electricity is more than ten times the short-run value. Price Elasticity and Decision Making Information about price elasticities can be extremely useful to managers as they contemplate pricing decisions, if demand is inelastic at the current price, a price decrease will result in a decrease in total revenue. Alternatively, reducing the price of a product with elastic demand would cause revenue to increase. The effect on total revenue would be the reverse for a price increase. However, if demand is unitary elastic, price changes will not change total revenues. However, a price reduction is not always the correct strategy when demand is elastic. The decision must also take into account the impact on the firm’s costs and profits. More will be
said about pricing strategy in Block 4. As another example of how knowledge of price elasticity may be useful, let’s
consider the demand for cigarettes. The price elasticity for cigarettes by age groups
has been found to be:
Age Group Price Elasticity
12-17 years – 1.40
20-25 years – 0.89
26-35 years – 0.47
36-74 years – 0.45These elasticities indicate that young smokers are much more responsive to price than are older smokers. This may be in part related to the fraction of income that goes towards the purchase of cigarettes. It may also reflect the degree to which physical/psychological addiction influences consumption. From the perspective of cigarette sellers, these results suggest that if all sellers increased prices proportionately, the total expenditure on cigarettes by adult smokers would increase. (Recall that when demand is inelastic, price and total revenue move in the same direction). Individual brands would be more price elastic than for the entire product class because each brand has other brands that represent potential substitutes;however, for the product class, there may be few good substitutes.
INCOME ELASTICITY OF DEMAND
The income elasticity of demand measures the responsiveness of sales to changesin income, ceteris paribus. It is defined as the percentage change in sales dividedby the corresponding percentage change in income. The methods used to calculatearc income elasticity (EI) and point income elasticity (eI)are as follows:
Given information on sales and income, the calculation of income elasticities is strictly analogous to the calculation of price elasticities. If the income elasticity of demand for a product is greater than one, the product is said to be income elastic; if it is less than one, the product is income inelastic. For normal goods, the income elasticity is greater than 0 because with rising incomes, consumers will purchase a greater quantity of such goods, ceteris paribus. If the income elasticity for a commodity is negative, the good is an inferior good; that is, people will choose to purchase less of the product when their income increases. Potatoes may represent examples of inferior goods for some households, as would purchases from the cheap stores. The reason is that some households consume certain goods only because of lack of purchasing power. As income increases it is possible the household will shift away from the purchase of these inferior goods. Income elasticity relationships can be summarized as follows: Normal goods are indicated by eI or EI > 0. Inferior goods are indicated by eI or
EI < 0.
If eI or EI > 1, the good is income elastic.
If eI or EI < 1, the good is income inelastic.
If eI or EI = 1, the good is unitarily income elastic.
To illustrate just one way in which income elasticity may be useful, consider the following situation. A firm has obtained a fairly reliable estimate of the projected percentage increase in income for its market area for the next year; let’s say 4.5 per cent. Managers know that sales are currently running at an annual rate of 200,000 units, and the marketing analysis group has estimated the arc income elasticity of demand for the product at 1.2. If other factors are expected to remain relatively constant, we can use this information as one input into projecting sales for the next year, as follows:E1=%Δ Q/ %Δ I
and subsequently
% ΔQ = (EI)(%ΔI)
% ΔQ = (1.2)(4.5)
% ΔQ = 5.4
Thus, next year’s sales would be projected to be 5.4 per cent above the current level, or 1.054 times this year’s sales: (1.054)(200,000) = 210,800 units Knowledge of income elasticities is also useful at different stages of a business cycle. For example, during periods of expansion, firms selling luxury products such as exotic vacations or big cars find demand for their products will increase at a rate that is faster than the rate of growth of incomes. However, during an economic recession demand may decrease rapidly for such products. Conversely, sellers of necessities such as basic food will not profit much during periods of economicprosperity, but will also find that their products are recession proof.
CROSS-PRICE ELASTICITY
The sales volume of one product may be influenced by the price of either substituteor complementary products. Cross-price elasticity of demand provides a means toquantify that type of influence. It is defined as the ratio of the percentage change insales of one product to the percentage change in price of another product. Therelevant arc (Ec) and point (ec) cross-price elasticities are determined as follows:
EI < 0.
If eI or EI > 1, the good is income elastic.
If eI or EI < 1, the good is income inelastic.
If eI or EI = 1, the good is unitarily income elastic.
To illustrate just one way in which income elasticity may be useful, consider the following situation. A firm has obtained a fairly reliable estimate of the projected percentage increase in income for its market area for the next year; let’s say 4.5 per cent. Managers know that sales are currently running at an annual rate of 200,000 units, and the marketing analysis group has estimated the arc income elasticity of demand for the product at 1.2. If other factors are expected to remain relatively constant, we can use this information as one input into projecting sales for the next year, as follows:E1=%Δ Q/ %Δ I
and subsequently
% ΔQ = (EI)(%ΔI)
% ΔQ = (1.2)(4.5)
% ΔQ = 5.4
Thus, next year’s sales would be projected to be 5.4 per cent above the current level, or 1.054 times this year’s sales: (1.054)(200,000) = 210,800 units Knowledge of income elasticities is also useful at different stages of a business cycle. For example, during periods of expansion, firms selling luxury products such as exotic vacations or big cars find demand for their products will increase at a rate that is faster than the rate of growth of incomes. However, during an economic recession demand may decrease rapidly for such products. Conversely, sellers of necessities such as basic food will not profit much during periods of economicprosperity, but will also find that their products are recession proof.
CROSS-PRICE ELASTICITY
The sales volume of one product may be influenced by the price of either substituteor complementary products. Cross-price elasticity of demand provides a means toquantify that type of influence. It is defined as the ratio of the percentage change insales of one product to the percentage change in price of another product. Therelevant arc (Ec) and point (ec) cross-price elasticities are determined as follows:
where the alphabetic subscripts differentiate between the two products involved. A negative coefficient of cross-price elasticity implies that a decrease in the price of product A results in an increase in sales of product B, or vice versa, we can conclude that the products are complementary to one another (such as cassette tape players and cassette tapes). Thus, when the coefficient of cross-price elasticity for two products is negative, the products are classified as complements.A similar line of reasoning leads to the conclusion that if the cross-price elasticity is positive, the products are substitutes. For example, an increase in the price of sugar would cause less sugar to be purchased, but would increase the sale of sugar substitutes. When we calculate the cross-price elasticity for this case, both the numerator and the denominator (% change in Q of sugar substitutes and % change in P of sugar, respectively) would have the same sign, and the coefficient would be positive. If two goods are unrelated, a change in the price of one will not affect the sales of
the other. The numerator of the cross-price elasticity ratio would be 0, and thus the coefficient of cross-price elasticity would be 0. In this case, the two commodities would be defined as independent. For example, consider the expected effect that a 10% increase in the price of eggs would have on the quantity of electronic calculator sales.
These relationships can be summarized as follows:
If ec or Ec > 0, goods are substitutes
If ec or Ec < 0, goods are complementary
If ec or Ec = 0, goods are independent
Cross price elasticities may not always be symmetrical. For example, consider two dailies, Times of India and the Hindustan Times competing in the Delhi market. Most analysts will agree that the two products are substitutes i.e. the cross price elasticity is positive. However, there is no reason to believe that the change in demand for the Times of India following a one percent change in the price of Hindustan times will be equal to the change in demand for Hindustan Times following a one per cent change in the price of the Times of India. Many large corporations produce several related products. Maruti produces many varieties of automobiles, Hindustan Lever produces many brands of soap and Gillette produces much type of razors. If Maruti reduces the price of it’s Alto model, sales of its old warhorse the Maruti 800 may decline. When a company sells related products, knowledge of cross elasticities can aid decision makers in assessing such impacts.
THE EFFECT OF ADVERTISING ON DEMAND
Advertising influences our attitudes towards the product or service being promoted.In most cases, the intent of a firm’s advertising is to stimulate sales of a particularproduct or product line. When Pepsi Cola Corporation decides to sponsor atelevision show or cricket match it hopes that doing so will increase the sales of itsproducts. Such product promotions have their impact on consumers through tastesand preferences.In addition to shifting the demand function to the right, advertising may have theeffect of making it somewhat more steep. The reason for this is thatadvertisements can create stronger consumer brand preferences, thus makingconsumers less sensitive to price changes for that product. This means that oneeffect of advertising can be to make the demand for a firm’s product more priceinelastic.To the extent that this is true, management has an increased ability toraise price without losing as many sales as would have been lost otherwise. Wehave seen that raising the product’s price will increase total revenue for the firm ifdemand is inelastic.
the other. The numerator of the cross-price elasticity ratio would be 0, and thus the coefficient of cross-price elasticity would be 0. In this case, the two commodities would be defined as independent. For example, consider the expected effect that a 10% increase in the price of eggs would have on the quantity of electronic calculator sales.
These relationships can be summarized as follows:
If ec or Ec > 0, goods are substitutes
If ec or Ec < 0, goods are complementary
If ec or Ec = 0, goods are independent
Cross price elasticities may not always be symmetrical. For example, consider two dailies, Times of India and the Hindustan Times competing in the Delhi market. Most analysts will agree that the two products are substitutes i.e. the cross price elasticity is positive. However, there is no reason to believe that the change in demand for the Times of India following a one percent change in the price of Hindustan times will be equal to the change in demand for Hindustan Times following a one per cent change in the price of the Times of India. Many large corporations produce several related products. Maruti produces many varieties of automobiles, Hindustan Lever produces many brands of soap and Gillette produces much type of razors. If Maruti reduces the price of it’s Alto model, sales of its old warhorse the Maruti 800 may decline. When a company sells related products, knowledge of cross elasticities can aid decision makers in assessing such impacts.
THE EFFECT OF ADVERTISING ON DEMAND
Advertising influences our attitudes towards the product or service being promoted.In most cases, the intent of a firm’s advertising is to stimulate sales of a particularproduct or product line. When Pepsi Cola Corporation decides to sponsor atelevision show or cricket match it hopes that doing so will increase the sales of itsproducts. Such product promotions have their impact on consumers through tastesand preferences.In addition to shifting the demand function to the right, advertising may have theeffect of making it somewhat more steep. The reason for this is thatadvertisements can create stronger consumer brand preferences, thus makingconsumers less sensitive to price changes for that product. This means that oneeffect of advertising can be to make the demand for a firm’s product more priceinelastic.To the extent that this is true, management has an increased ability toraise price without losing as many sales as would have been lost otherwise. Wehave seen that raising the product’s price will increase total revenue for the firm ifdemand is inelastic.