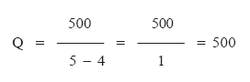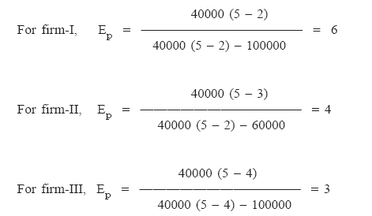INTRODUCTION
In previous unit , you have learnt different cost concepts used by managers in decision making process, the relationship between these concepts, and the distinction between accounting costs and economic costs. We will continue the analysis of costs in this unit also. To make wise decisions concerning how much to produce and what prices to charge, a manager must understand the relationship between firm’s output rate and its costs. In this unit, we learn to analyse in detail the nature of this relationship, both in short run and long run.
SHORT-RUN COST FUNCTIONS
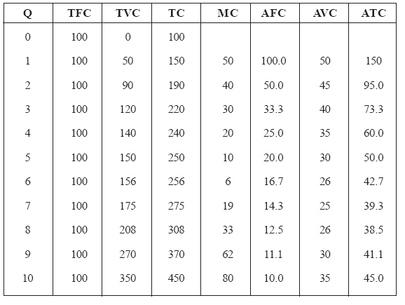
In Unit 8 we have distinguished between the short run and the long run. Wealso distinguished between fixed costs and variable costs. The distinctionbetween fixed and variable costs is of great significance to the businessmanager. Variable costs are those costs, which the business manager cancontrol or alter in the short run by changing levels of production. On the otherhand, fixed costs are clearly beyond business manager’s control, such costs areincurred in the short run and must be paid regardless of output.Total CostsThree concepts of total cost in the short run must be considered: total fixedcost (TFC), total variable cost (TVC), and total cost (TC). Total fixed costsare the total costs per period of time incurred by the firm for fixed inputs.Since the amount of the fixed inputs is fixed, the total fixed cost will be thesame regardless of the firm’s output rate. Table below shows the costs of a firmin the short run. According to this table, the firm’s total fixed costs are Rs. 100.The firm’s total fixed cost function is shown graphically in Figure
In previous unit , you have learnt different cost concepts used by managers in decision making process, the relationship between these concepts, and the distinction between accounting costs and economic costs. We will continue the analysis of costs in this unit also. To make wise decisions concerning how much to produce and what prices to charge, a manager must understand the relationship between firm’s output rate and its costs. In this unit, we learn to analyse in detail the nature of this relationship, both in short run and long run.
SHORT-RUN COST FUNCTIONS
In Unit 8 we have distinguished between the short run and the long run. Wealso distinguished between fixed costs and variable costs. The distinctionbetween fixed and variable costs is of great significance to the businessmanager. Variable costs are those costs, which the business manager cancontrol or alter in the short run by changing levels of production. On the otherhand, fixed costs are clearly beyond business manager’s control, such costs areincurred in the short run and must be paid regardless of output.Total CostsThree concepts of total cost in the short run must be considered: total fixedcost (TFC), total variable cost (TVC), and total cost (TC). Total fixed costsare the total costs per period of time incurred by the firm for fixed inputs.Since the amount of the fixed inputs is fixed, the total fixed cost will be thesame regardless of the firm’s output rate. Table below shows the costs of a firmin the short run. According to this table, the firm’s total fixed costs are Rs. 100.The firm’s total fixed cost function is shown graphically in Figure
Total variable costs are the total costs incurred by the firm for variable inputs. To obtain total variable cost we must know the price of the variable inputs.
Suppose if we have two variable inputs viz. labour (V1) and raw material (V2) and the corresponding prices of these inputs are P1 and P2, then the total
variable cost (TVC) = P1 * V1 + P2 * V2. They go up as the firm’s output rises, since higher output rates require higher variable input rates, which mean
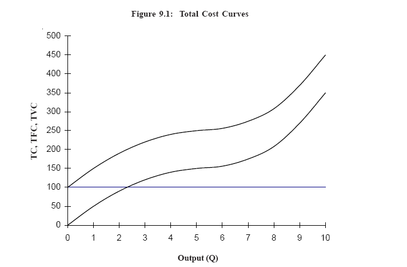
bigger variable costs. The firm’s total variable cost function corresponding to the data given in Table is shown graphically in Figure. Finally, total costs are the sum of total fixed costs and total variable costs. To derive the total cost column in Table 9.1, add total fixed cost and total variable cost at each output. The firm’s total cost function corresponding to the data given in Table is shown graphically in Figure 9.1. Since total fixed costsare constant, the total fixed cost curve is simply a horizontal line at Rs.100.And because total cost is the sum of total variable costs and total fixed costs,
the total cost curve has the same shape as the total variable cost curve but lies above it by a vertical distance of Rs. 100.
Corresponding to our discussion above we can define the following for the short run:
TC = TFC + TVC
Where,
TC = total cost
TFC = total fixed costsTVC = total variable costs.
Average Fixed Costs
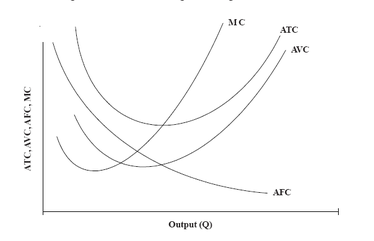
While the total cost functions are of great importance, managers must beinterested as well in the average cost functions and the marginal cost functionas well. There are three average cost concepts corresponding to the three totalcost concepts. These are average fixed cost (AFC), average variable cost(AVC), and average total cost (ATC). Figure 9.2 show typical average fixedcost function graphically. Average fixed cost is the total fixed cost divided byoutput. Average fixed cost declines as output (Q) increases. Thus we canwrite average fixed cost as:AFC = TFC/Q
Suppose if we have two variable inputs viz. labour (V1) and raw material (V2) and the corresponding prices of these inputs are P1 and P2, then the total
variable cost (TVC) = P1 * V1 + P2 * V2. They go up as the firm’s output rises, since higher output rates require higher variable input rates, which mean
bigger variable costs. The firm’s total variable cost function corresponding to the data given in Table is shown graphically in Figure. Finally, total costs are the sum of total fixed costs and total variable costs. To derive the total cost column in Table 9.1, add total fixed cost and total variable cost at each output. The firm’s total cost function corresponding to the data given in Table is shown graphically in Figure 9.1. Since total fixed costsare constant, the total fixed cost curve is simply a horizontal line at Rs.100.And because total cost is the sum of total variable costs and total fixed costs,
the total cost curve has the same shape as the total variable cost curve but lies above it by a vertical distance of Rs. 100.
Corresponding to our discussion above we can define the following for the short run:
TC = TFC + TVC
Where,
TC = total cost
TFC = total fixed costsTVC = total variable costs.
Average Fixed Costs
While the total cost functions are of great importance, managers must beinterested as well in the average cost functions and the marginal cost functionas well. There are three average cost concepts corresponding to the three totalcost concepts. These are average fixed cost (AFC), average variable cost(AVC), and average total cost (ATC). Figure 9.2 show typical average fixedcost function graphically. Average fixed cost is the total fixed cost divided byoutput. Average fixed cost declines as output (Q) increases. Thus we canwrite average fixed cost as:AFC = TFC/Q
Average Variable Costs
Average variable cost is the total variable cost divided by output. Figure shows the average variable cost function graphically. At first, output increases
resulting in decrease in average variable cost, but beyond a point, they result in higher average variable cost.AVC = TVC/QAverage Total Cost
Average total cost (ATC) is the sum of the average fixed cost and average variable cost. In other words, ATC is total cost divided by output. Thus,
ATC = AFC + AVC = —TC—Q
Figure shows the average total cost function graphically. Since ATC is sum of the AFC and AVC, ATC curve always exceeds AVC curve. Also, since
AFC falls as output increases, AVC and ATC get closer as output rises. Note that ATC curve is nearer the AFC curve at initial levels of output, but is nearer
the AVC curve at later levels of output. This indicates that at lower levels of output fixed costs are more important part of the total cost, while at higherlevels of output the variable element of cost becomes more important.Marginal CostMarginal cost (MC) is the addition to either total cost or total variable costresulting from the addition of one unit of output. Thus,MC = — W—TC— = —WT—V—CWQ WQWhere,MC = marginal costW Q = change in outputW TC = change in total cost due to change in outputWTVC = change in total variable cost due to change in outputThe two definitions are the same because, when output increases, total costincreases by the same amount as the increase in total variable cost (since fixedcost remains constant). Figure shows the marginal cost functiongraphically. At low output levels, marginal cost may decrease with increase inoutput, but after reaching a minimum, it goes up with further increase in output.The reason for this behaviour is found in diminishing marginal returns.The marginal cost concept is very crucial from the manager’s point of view.Marginal cost is a strategic concept because it designates those costs overwhich the firm has the most direct control. More specifically, MC indicatesthose costs which are incurred in the production of the last unit of output andtherefore, also the cost which can be “saved” by reducing total output by thelast unit. Average cost figures do not provide this information. A firm’sdecisions as to what output level to produce is largely influenced by its marginalcost. When coupled with marginal revenue, which indicates the change inrevenue from one more or one less unit of output, marginal cost allows a firmto determine whether it is profitable to expand or contract its level ofproduction.Relationship between Marginal Cost and Average CostsThe relationships between the various average and marginal cost curves areillustrated in Figure. The figure shows typical AFC, AVC, ATC, and MCcurves but is not drawn to scale for the data given in Table . The MC cuts both AVC and ATC at their minimum. When both the MC and AVC are falling, AVC will fall at a slower rate. When both the MC and AVC are rising, MC will rise at a faster rate. As a result, MC will attain its minimum before the AVC. In other words, when MC is less than AVC, the AVC will fall, and when MC exceeds AVC, AVC will rise. This means that as long as MC lies below AVC, the latter will fall and where MC is above AVC, AVC will rise. Therefore, at the point of intersection where MC = AVC, AVC has just ceased to fall and attained its minimum, but has not yet begun to rise. Similarly, the MC curve cuts the ATC curve at the latter’s minimum point. This is because MC can be defined as the addition either to TC or TVC resulting from one more unit of output. However, no such relationship exists between MC and AFC, because the two are not related; MC by definition includes only those costs which change with output, and FC by definition is independent of output.
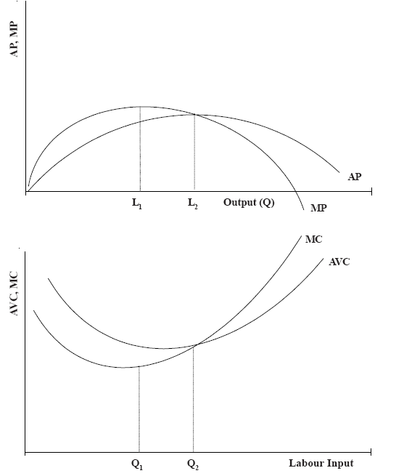
Relationship between Average Product and Marginal Product, and Average Variable Cost and Marginal Cost
There is a straightforward relationship between factor productivity and outputcosts. To see this, let us consider a single variable factor L say labour. Allother inputs are fixed. AP and MP will denote the average and marginalproducts of labour, respectively. If W is the wage rate and L is the quantityof labour, thenTVC = W * LHence, if Q is the output,AVC=TVC/Q=W{L/Q} Consequently, since Q/W is the average product (AP), AVC = W/APAlso, WTVC = W * WL (W does not change and is assumed to be given.)Dividing by WQ we get MC=TVC/Q=W{L/Q} But, marginal product (MP) = WQ/ W L. Hence, MC = W/MPFigure 9.3 shows the relationship between average product and marginalproduct, and average variable cost and marginal cost. The relationship AVC =W/AP shows that AVC is at a minimum when AP is at maximum. Similarly,the relationship MC = W/MP shows that MC is at a minimum when MP is ata maximum. Also, when AP is at a maximum, AP = MP. Hence, when AVCis at a minimum, AVC = MC. It is clearly shown that when MP is rising, MCis falling. And when MP is falling, MC is rising.The relevant costs to be considered for decision-making will differ from onesituation to the other depending on the problem faced by the manager. Ingeneral, the TC concept is quite useful in finding out the breakeven quantity ofoutput. The TC concept is also used to find out whether firm is making profitsor not. The AC concept is important for calculating the per unit profit of abusiness firm. The MC concept is essential to decide whether a firm shouldexpand its production or not.
Average variable cost is the total variable cost divided by output. Figure shows the average variable cost function graphically. At first, output increases
resulting in decrease in average variable cost, but beyond a point, they result in higher average variable cost.AVC = TVC/QAverage Total Cost
Average total cost (ATC) is the sum of the average fixed cost and average variable cost. In other words, ATC is total cost divided by output. Thus,
ATC = AFC + AVC = —TC—Q
Figure shows the average total cost function graphically. Since ATC is sum of the AFC and AVC, ATC curve always exceeds AVC curve. Also, since
AFC falls as output increases, AVC and ATC get closer as output rises. Note that ATC curve is nearer the AFC curve at initial levels of output, but is nearer
the AVC curve at later levels of output. This indicates that at lower levels of output fixed costs are more important part of the total cost, while at higherlevels of output the variable element of cost becomes more important.Marginal CostMarginal cost (MC) is the addition to either total cost or total variable costresulting from the addition of one unit of output. Thus,MC = — W—TC— = —WT—V—CWQ WQWhere,MC = marginal costW Q = change in outputW TC = change in total cost due to change in outputWTVC = change in total variable cost due to change in outputThe two definitions are the same because, when output increases, total costincreases by the same amount as the increase in total variable cost (since fixedcost remains constant). Figure shows the marginal cost functiongraphically. At low output levels, marginal cost may decrease with increase inoutput, but after reaching a minimum, it goes up with further increase in output.The reason for this behaviour is found in diminishing marginal returns.The marginal cost concept is very crucial from the manager’s point of view.Marginal cost is a strategic concept because it designates those costs overwhich the firm has the most direct control. More specifically, MC indicatesthose costs which are incurred in the production of the last unit of output andtherefore, also the cost which can be “saved” by reducing total output by thelast unit. Average cost figures do not provide this information. A firm’sdecisions as to what output level to produce is largely influenced by its marginalcost. When coupled with marginal revenue, which indicates the change inrevenue from one more or one less unit of output, marginal cost allows a firmto determine whether it is profitable to expand or contract its level ofproduction.Relationship between Marginal Cost and Average CostsThe relationships between the various average and marginal cost curves areillustrated in Figure. The figure shows typical AFC, AVC, ATC, and MCcurves but is not drawn to scale for the data given in Table . The MC cuts both AVC and ATC at their minimum. When both the MC and AVC are falling, AVC will fall at a slower rate. When both the MC and AVC are rising, MC will rise at a faster rate. As a result, MC will attain its minimum before the AVC. In other words, when MC is less than AVC, the AVC will fall, and when MC exceeds AVC, AVC will rise. This means that as long as MC lies below AVC, the latter will fall and where MC is above AVC, AVC will rise. Therefore, at the point of intersection where MC = AVC, AVC has just ceased to fall and attained its minimum, but has not yet begun to rise. Similarly, the MC curve cuts the ATC curve at the latter’s minimum point. This is because MC can be defined as the addition either to TC or TVC resulting from one more unit of output. However, no such relationship exists between MC and AFC, because the two are not related; MC by definition includes only those costs which change with output, and FC by definition is independent of output.
Relationship between Average Product and Marginal Product, and Average Variable Cost and Marginal Cost
There is a straightforward relationship between factor productivity and outputcosts. To see this, let us consider a single variable factor L say labour. Allother inputs are fixed. AP and MP will denote the average and marginalproducts of labour, respectively. If W is the wage rate and L is the quantityof labour, thenTVC = W * LHence, if Q is the output,AVC=TVC/Q=W{L/Q} Consequently, since Q/W is the average product (AP), AVC = W/APAlso, WTVC = W * WL (W does not change and is assumed to be given.)Dividing by WQ we get MC=TVC/Q=W{L/Q} But, marginal product (MP) = WQ/ W L. Hence, MC = W/MPFigure 9.3 shows the relationship between average product and marginalproduct, and average variable cost and marginal cost. The relationship AVC =W/AP shows that AVC is at a minimum when AP is at maximum. Similarly,the relationship MC = W/MP shows that MC is at a minimum when MP is ata maximum. Also, when AP is at a maximum, AP = MP. Hence, when AVCis at a minimum, AVC = MC. It is clearly shown that when MP is rising, MCis falling. And when MP is falling, MC is rising.The relevant costs to be considered for decision-making will differ from onesituation to the other depending on the problem faced by the manager. Ingeneral, the TC concept is quite useful in finding out the breakeven quantity ofoutput. The TC concept is also used to find out whether firm is making profitsor not. The AC concept is important for calculating the per unit profit of abusiness firm. The MC concept is essential to decide whether a firm shouldexpand its production or not.
LONG-RUN COST FUNCTIONS
In the long run, all inputs are variable, and a firm can have a number of alternative plant sizes and levels of output that it wants. There are no fixed
cost functions (total or average) in the long run, since no inputs are fixed. A useful way of looking at the long run is to consider it a planning horizon. The
long run cost curve is also called planning curve because it helps the firm in future decision making process.
In the long run, all inputs are variable, and a firm can have a number of alternative plant sizes and levels of output that it wants. There are no fixed
cost functions (total or average) in the long run, since no inputs are fixed. A useful way of looking at the long run is to consider it a planning horizon. The
long run cost curve is also called planning curve because it helps the firm in future decision making process.
The long run cost output relationship can be shown with the help of a long run cost curve. The long run average cost curve (LRAC) is derived from short
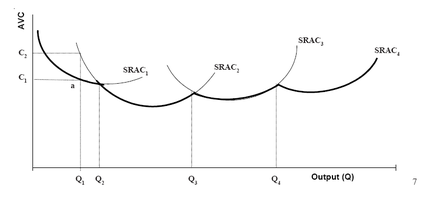
run average cost curves (SRAC). Let us illustrate this with the help of a simple example. A firm faces a choice of production with three different
plant sizes viz. plant size-1 (small size), plant size-2 (medium size), plant size-3 (large size), and plant size-4 (very large size). The short run average cost
functions shown in Figure 9.4 (SRAC1, SRAC2, SRAC3, and SRAC4) are associated with each of these plants discrete scale of operation. The long run
average cost function for this firm is defined by the minimum average cost of each level of output. For example, output rate Q1 could be produced by the
plant size-1 at an average cost of C1 or by plant size-2 at a cost of C2. Clearly, the average cost is lower for plant size-1, and thus point a is one point
on the long run average cost curve. By repeating this process for various rates of output, the long run average cost is determined. For output rates of
zero to Q2 plant size-1is the most efficient and that part of SRAC1 is part of the long run cost function. For output rates of Q2 to Q3 plant size-2 is the
most efficient, and for output rates Q3 to Q4, plant size-3 is the most efficient. The scallop-shaped curve shown in boldface in Figure 9.4 is the long run
average cost curve for this firm. This boldfaced curve is called an envelope curve (as it envelopes short run average cost curves). Firms plan to be on this
envelope curve in the long run. Consider a firm currently operating plant size-2 and producing Q1 units at a cost of C2 per unit. If output is expected to
remain at Q1, the firm will plan to adjust to plant size-1, thus reducing average cost to C1. Most firms will have many alternative plant sizes to choose from, and there is a short run average cost curve corresponding to each. A few of the short run average cost curves for these plants are shown in Figure although many more may exist. Only one point of a very small arc of each short run cost curve will lie on the long run average cost function. Thus long run average cost curve can be shown as the smooth U-shaped curve. Corresponding to this long run average cost curve is a long run marginal cost (LRMC) curve, which intersects LRAC at its minimum point a, which is also the minimum point of short run average cost curve 4 (SRAC4). Thus, at a point a and only at a point a, the following unique result occurs:
SRAC = SRMC when LRAC = LRMC
run average cost curves (SRAC). Let us illustrate this with the help of a simple example. A firm faces a choice of production with three different
plant sizes viz. plant size-1 (small size), plant size-2 (medium size), plant size-3 (large size), and plant size-4 (very large size). The short run average cost
functions shown in Figure 9.4 (SRAC1, SRAC2, SRAC3, and SRAC4) are associated with each of these plants discrete scale of operation. The long run
average cost function for this firm is defined by the minimum average cost of each level of output. For example, output rate Q1 could be produced by the
plant size-1 at an average cost of C1 or by plant size-2 at a cost of C2. Clearly, the average cost is lower for plant size-1, and thus point a is one point
on the long run average cost curve. By repeating this process for various rates of output, the long run average cost is determined. For output rates of
zero to Q2 plant size-1is the most efficient and that part of SRAC1 is part of the long run cost function. For output rates of Q2 to Q3 plant size-2 is the
most efficient, and for output rates Q3 to Q4, plant size-3 is the most efficient. The scallop-shaped curve shown in boldface in Figure 9.4 is the long run
average cost curve for this firm. This boldfaced curve is called an envelope curve (as it envelopes short run average cost curves). Firms plan to be on this
envelope curve in the long run. Consider a firm currently operating plant size-2 and producing Q1 units at a cost of C2 per unit. If output is expected to
remain at Q1, the firm will plan to adjust to plant size-1, thus reducing average cost to C1. Most firms will have many alternative plant sizes to choose from, and there is a short run average cost curve corresponding to each. A few of the short run average cost curves for these plants are shown in Figure although many more may exist. Only one point of a very small arc of each short run cost curve will lie on the long run average cost function. Thus long run average cost curve can be shown as the smooth U-shaped curve. Corresponding to this long run average cost curve is a long run marginal cost (LRMC) curve, which intersects LRAC at its minimum point a, which is also the minimum point of short run average cost curve 4 (SRAC4). Thus, at a point a and only at a point a, the following unique result occurs:
SRAC = SRMC when LRAC = LRMC
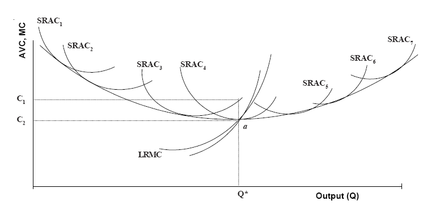
The long run cost curve serves as a long run planning mechanism for the firm. It shows the least per unit cost at any output can be produced after the firm
has had time to make all appropriate adjustments in its plant size. For example, suppose that the firm is operating on short run average cost curve
SRAC3 as shown in Figure 9.5, and the firm is currently producing an output of Q*. By using SRAC3, it is seen that the firm’s average cost is C2.
Clearly, if projections of future demand indicate that the firm could expect to continue selling Q* units per period at the market price, profit could be
increased significantly by increasing the scale of plant to the size associated with short run average cost curve SRAC4. With this plant, average cost for an
output rate of Q* would be C2 and the firm’s profit per unit would increase by C2 – C1. Thus, total profit would increase by (C2 – C1) * Q*.
The U-shape of the LRAC curve reflects the laws of returns to scale.According to these laws, the cost per unit of production decreases as plant size
increases due to the economies of scale, which the larger plant sizes make possible. But the economies of scale exist only up to a certain size of plant,
known as the optimum plant size where all possible economies of scale are fully exploited. Beyond the optimum plant size, diseconomies of scale arise due
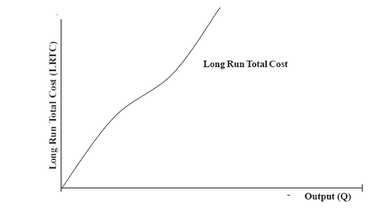
to managerial inefficiencies. As plant size increases beyond a limit, the control, the feedback of information at different levels and decision-making process becomes less efficient. This makes the LRAC curve turn upwards. Given the LRAC in Figure , we can say that there are increasing returns to scale up to Q* and decreasing returns to scale beyond Q*. Therefore, the point Q* is the point of optimum output and the corresponding plant size-4 is the optimum plant size. If you have long run average cost of producing a given output, you can readily derive the long run total cost (LRTC) of the output, since the long run total cost is simply the product of long run average cost and output.
Thus, LRTC = LRAC * Q.
Figure shows the relationship between long run total cost and output. Given the long run total cost function you can readily derive the long run
marginal cost function, which shows the relationship between output and the cost resulting from the production of the last unit of output, if the firm has time to make the optimal changes in the quantities of all inputs used.
has had time to make all appropriate adjustments in its plant size. For example, suppose that the firm is operating on short run average cost curve
SRAC3 as shown in Figure 9.5, and the firm is currently producing an output of Q*. By using SRAC3, it is seen that the firm’s average cost is C2.
Clearly, if projections of future demand indicate that the firm could expect to continue selling Q* units per period at the market price, profit could be
increased significantly by increasing the scale of plant to the size associated with short run average cost curve SRAC4. With this plant, average cost for an
output rate of Q* would be C2 and the firm’s profit per unit would increase by C2 – C1. Thus, total profit would increase by (C2 – C1) * Q*.
The U-shape of the LRAC curve reflects the laws of returns to scale.According to these laws, the cost per unit of production decreases as plant size
increases due to the economies of scale, which the larger plant sizes make possible. But the economies of scale exist only up to a certain size of plant,
known as the optimum plant size where all possible economies of scale are fully exploited. Beyond the optimum plant size, diseconomies of scale arise due
to managerial inefficiencies. As plant size increases beyond a limit, the control, the feedback of information at different levels and decision-making process becomes less efficient. This makes the LRAC curve turn upwards. Given the LRAC in Figure , we can say that there are increasing returns to scale up to Q* and decreasing returns to scale beyond Q*. Therefore, the point Q* is the point of optimum output and the corresponding plant size-4 is the optimum plant size. If you have long run average cost of producing a given output, you can readily derive the long run total cost (LRTC) of the output, since the long run total cost is simply the product of long run average cost and output.
Thus, LRTC = LRAC * Q.
Figure shows the relationship between long run total cost and output. Given the long run total cost function you can readily derive the long run
marginal cost function, which shows the relationship between output and the cost resulting from the production of the last unit of output, if the firm has time to make the optimal changes in the quantities of all inputs used.
ECONOMIES AND DIS ECONOMIES OF SCALE
We have seen in the preceding section that larger plant will lead to lower average cost in the long run. However, beyond some point, successively larger
plants will mean higher average costs. Exactly, why is the long run average cost (LRAC) curve U-shaped? What determines the shape of LARC curve?
This point needs further explanation. It must be emphasized here that the law of diminishing returns is not applicable in the long run as all inputs are variable. Also, we assume that resource prices are constant. What then, is our explanation? The U-shaped LRAC curve is explainable in terms of what economists call economies of scale and dis economies of scale. Economies and diseconomies of scale are concerned with behaviour of average cost curve as the plant size is increased. If LRAC declines as output increases, then we say that the firm enjoys economies of scale. If, instead, the LRAC increases as output increases, then we have diseconomies of scale. Finally, if LRAC is constant as output increases, then we have constant returns to scale implying we have neither economies of scale nor diseconomies of scale. Economies of scale explain the down sloping part of the LRAC curve. As the size of the plant increases, LRAC typically declines over some range of output for a number of reasons. The most important is that, as the scale of output is
expanded, there is greater potential for specialization of productive factors.This is most notable with regard to labour but may apply to other factors as
well. Other factors contributing to declining LRAC include ability to use more advanced technologies and more efficient capital equipment; managerial
specialization; opportunity to take advantage of lower costs (discounts) for some inputs by purchasing larger quantities; effective utilization of by products,etc. But, after sometime, expansion of a firm’s output may give rise to diseconomies, and therefore, higher average costs. Further expansion of output beyond a reasonable level may lead to problems of over crowding of labour, managerial inefficiencies, etc., pushing up the average costs.
In this section, we examined the shape of the LRAC curve. In other words, we have analysed the relationship between firm’s output and its long run
average costs. The economies of scale and diseconomies of scale are some times called as internal economies of scale and internal diseconomies of
scale respectively. This is because the changes in long run average costs result solely from the individual firm’s adjustment of its output. On the other
hand, there may exist external economies of scale. The external economies also help in cutting down production costs. With the expansion of an industry,
certain specialized firms also come up for working up the by-products and waste materials. Similarly, with the expansion of the industry, certain
specialized units may come up for supplying raw material, tools, etc., to the firms in the industry. Moreover, they can combine together to undertake
research etc., whose benefit will accrue to all firms in the industry. Thus, a firm benefits from expansion of the industry as a whole. These benefits are
external to the firm, in the sense that these have arisen not because of any effort on the part of the firm but have accrued to it due to expansion of
industry as a whole. All these external economies help in reducing production costs.Economies of scale are often measured in terms of cost-output elasticity, Ec. Ec is the percentage change in the average cost of production resulting from a one percent increase in output:
Ec = (WTC/TC) / (WQ/Q) = (WTC/ WQ) / (TC/Q) = MC/AC Clearly,
Ec is equal to one when marginal and average costs are equal. This means costs increase proportionately with output, and there are neither economies nor diseconomies of scale. When there are economies of scale MC will be less than AC (both are declining) and Ec is less than one. Finally, when there are diseconomies of scale, MC is greater than AC, and Ec isgreater than one.
ECONOMIES OF SCOPE
According to the concept of economies of scale, cost advantages follow the increase in volume of production or what is called the scale of output. On the
other hand, according to the concept of economies of scope, such cost advantages may follow from a variety of output. For example, many firms
produce more than one product and the products are closely related to one another — an automobile company produces scooters and cars, and a university
produces teaching and research. A firm is likely to enjoy production or cost advantages when it produces two or more products. These advantages could
result from the joint use of inputs or production facilities, joint marketing programs, or possibly the cost savings of a common administration. Examples
of joint products are mutton and wool, eggs and chicken, fertilizer, etc. Therefore, economies of scope exist when the cost of producing two (or more)
products jointly is less than the cost of producing a single product. To measure the degree to which there are economies of scope, we should know what
percentage of the cost of production is saved when two (or more) products are produced jointly rather than individually. The following equation gives the
degree of economies of scope (SC) that measures the savings in cost:
SC =C (Q1) + C (Q2) – C (Q1 + Q2)/C (Q1 + Q2)
Here, C (Q1) represents the cost of producing output Q1, C (Q2) the cost of producing output Q2, and C (Q1, Q2) the joint cost of producing both outputs
(Q1 + Q2). For example, a firm produces 10000 TV sets and 5000 Radio sets per year at a cost of Rs.8.40 crores, and another firm produces 10000 TV sets only, then the cost would be Rs.10.00 crores, and if it produced 5000 Radio sets only, then the cost would be Rs. 0.50 crores. In this case, the cost of producing both the TV and Radio sets is less than the total cost of producing each separately. Thus, there are economies of scope. Thus,
0 SC =10.00 + 0.50 – 8.4/8.40= 0.25
Which means that there is a 25% saving of cost by going for joint production.With economies of scope, the joint cost is less than the sum of the individual
costs, so that SC is greater than 0. With diseconomies of scope, SC is negative. In general, the larger the value of SC, the greater is the economiesof scope.
APPLICATION OF COST ANALYSIS
In the previous sections of this unit we discussed total, marginal, and average cost curves for both short run and long run. The relationships between these cost curves have a very wide range of applications for managerial use. Here we will discuss a few applications of these concepts. Determining Optimum Output Level Earlier we have seen that the optimum output level is the point where average cost is minimum. In other words, the optimum output level is the point whereaverage cost equals marginal cost. Consider the following example.
Breakeven Output Level
An analytical tool frequently employed by managerial economists is the breakeven chart, an important application of cost functions. The breakeven
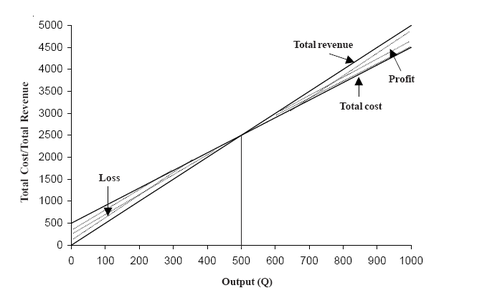
chart illustrates at what level of output in the short run, the total revenue just covers total costs. Generally, a breakeven chart assumes that the firm’s
average variable costs are constant in the relevant output range; hence, the firm’s total cost function is assumed to be a straight line. Since variable cost is constant, the marginal cost is also constant and equals to average variable cost. Figure shows the breakeven chart of a firm. Here, it is assumed that the price of the product will not be affected by the quantity of sales. Therefore, the total revenue is proportional to output. Consequently, the total revenue curve is a straight line through the origin. The firm’s fixed cost is Rs. 500, variable cost per unit is Rs. 4 and the unit sales price of output is Rs. 5. The breakeven chart, which combines the total cost function and the total revenue curve, shows profit or loss resulting from each sales level. For example, Figure shows that if the firm sells 200 units of output it will make a loss of Rs. 300. The chart also shows the breakeven point, the output level that must be reached if the firm is to avoid losses. It can be seen from the figure, the breakeven point is 500 units of output. Beyond 500 units of output the firm makes profit.
An analytical tool frequently employed by managerial economists is the breakeven chart, an important application of cost functions. The breakeven
chart illustrates at what level of output in the short run, the total revenue just covers total costs. Generally, a breakeven chart assumes that the firm’s
average variable costs are constant in the relevant output range; hence, the firm’s total cost function is assumed to be a straight line. Since variable cost is constant, the marginal cost is also constant and equals to average variable cost. Figure shows the breakeven chart of a firm. Here, it is assumed that the price of the product will not be affected by the quantity of sales. Therefore, the total revenue is proportional to output. Consequently, the total revenue curve is a straight line through the origin. The firm’s fixed cost is Rs. 500, variable cost per unit is Rs. 4 and the unit sales price of output is Rs. 5. The breakeven chart, which combines the total cost function and the total revenue curve, shows profit or loss resulting from each sales level. For example, Figure shows that if the firm sells 200 units of output it will make a loss of Rs. 300. The chart also shows the breakeven point, the output level that must be reached if the firm is to avoid losses. It can be seen from the figure, the breakeven point is 500 units of output. Beyond 500 units of output the firm makes profit.
Breakeven charts are used extensively for managerial decision process. Under right conditions, breakeven charts can produce useful projections of the effect of the output rate on costs, revenue and profits. For example, a firm may use breakeven chart to determine the effect of projected decline in sales or profits. On the other hand, the firm may use it to determine how many units of a particular product it must sell in order to breakeven or to make a particular level of profit. However, breakeven charts must be used with caution, since the assumptions underlying them, sometimes, may not be appropriate. If the product price is highly variable or if costs are difficult to predict, the estimated total cost function and revenue curves may be subject to these errors. We can analyse the breakeven output with familiar algebraic equations.
Here Q stands for breakeven volume of output. Multiplying Q with price (P) we get the breakeven value of output. In the case of our example given in
Figure 9.7, FC = Rs. 500, P = Rs. 5 and AVC = Rs. 4. Consequently,
Figure 9.7, FC = Rs. 500, P = Rs. 5 and AVC = Rs. 4. Consequently,
Therefore, the breakeven output (Q) will be 500 units. Similarly, the breakeven output value will be Rs.2500 (P * Q = Rs. 5 * 500).
Profit Contribution Analysis
In making short run decisions, firms often find it useful to carry out profit contribution analysis. The profit contribution is the difference between price
and average variable cost (P – AVC). That is, revenue on the sale of a unit of output after variable costs are covered represents a contribution towards
profit. In our example since price is Rs.5 and average variable cost is Rs.4, the profit contribution per unit of output will be Rs.1 (Rs.5 – Rs.4). At low
rates of output the firm may be losing money because fixed costs have not yet been covered by the profit contribution. Thus, at these low rates of output,
profit contribution is used to cover fixed costs. After fixed costs are covered, the firm will be earning a profit. A manager wants to know the output rate necessary to cover all fixed costs and to earn a ‘required’ profit (pR). Assume that both price and AVC are constant. Profit is equal to revenue less the sum of total variable costs and fixed costs. Thus pR = P * Q – [(Q * AVC) + FC] Solving this equation for Q gives a relation that can be used to determine therate of output necessary to generate a specified rate of profit. ThusProduction and Q =P – AVC /FC + pR
To illustrate how profit contribution analysis can be used, suppose that the firm in our example (where FC = Rs. 500, P = Rs. 4 and AVC = Rs. 2.50) wants
to determine how many units of output it will have to produce and sell to earn a profit of Rs.10, 000. To generate this profit, an output rate of 10,500 units isrequired; that is,Q= Rs 500 + Rs 10,000/Rs 5- Rs 4 = 10,500.
Operating Leverage
Managers must make comparisons among alternative systems of production. Should one type of plant be replaced by another? Breakeven analysis can be
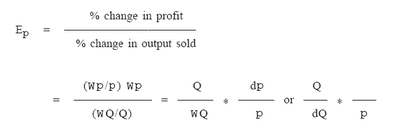
extended to help make such comparisons more effective. Consider the degree of operating leverage (Ep), which is defined as the percentage change inprofit resulting from a 1% change in the number of units of product sold. Thus
Profit Contribution Analysis
In making short run decisions, firms often find it useful to carry out profit contribution analysis. The profit contribution is the difference between price
and average variable cost (P – AVC). That is, revenue on the sale of a unit of output after variable costs are covered represents a contribution towards
profit. In our example since price is Rs.5 and average variable cost is Rs.4, the profit contribution per unit of output will be Rs.1 (Rs.5 – Rs.4). At low
rates of output the firm may be losing money because fixed costs have not yet been covered by the profit contribution. Thus, at these low rates of output,
profit contribution is used to cover fixed costs. After fixed costs are covered, the firm will be earning a profit. A manager wants to know the output rate necessary to cover all fixed costs and to earn a ‘required’ profit (pR). Assume that both price and AVC are constant. Profit is equal to revenue less the sum of total variable costs and fixed costs. Thus pR = P * Q – [(Q * AVC) + FC] Solving this equation for Q gives a relation that can be used to determine therate of output necessary to generate a specified rate of profit. ThusProduction and Q =P – AVC /FC + pR
To illustrate how profit contribution analysis can be used, suppose that the firm in our example (where FC = Rs. 500, P = Rs. 4 and AVC = Rs. 2.50) wants
to determine how many units of output it will have to produce and sell to earn a profit of Rs.10, 000. To generate this profit, an output rate of 10,500 units isrequired; that is,Q= Rs 500 + Rs 10,000/Rs 5- Rs 4 = 10,500.
Operating Leverage
Managers must make comparisons among alternative systems of production. Should one type of plant be replaced by another? Breakeven analysis can be
extended to help make such comparisons more effective. Consider the degree of operating leverage (Ep), which is defined as the percentage change inprofit resulting from a 1% change in the number of units of product sold. Thus
If the price of output is constant regardless of the rate of output, the change in degree of operating leverage depends on three variables: the rate of output, the level of fixed costs, and variable cost per unit of output. This can be seen by substituting the above equation for profit with
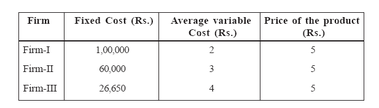
Example: Consider three firms I, II and III having the following fixed costs, average variable costs and price of the product.
Firm-I has more fixed cost than firm-II, and firm-III. However, Firm-I has less average costs than firm-II, and firm-III. Essentially, firm-I has substituted
capital (fixed costs) for labour and materials (variable costs) with the introduction more mechanized machines. On the other hand, firm-III has less
fixed costs and more average variable costs when compared to other two plants because firm-III has less mechanized machines. The firm-II occupies
middle position in terms of fixed costs and average variable costs. In comparing these plants, we use the degree of operating leverage. Suppose
for all the three plants Q = 40,000
capital (fixed costs) for labour and materials (variable costs) with the introduction more mechanized machines. On the other hand, firm-III has less
fixed costs and more average variable costs when compared to other two plants because firm-III has less mechanized machines. The firm-II occupies
middle position in terms of fixed costs and average variable costs. In comparing these plants, we use the degree of operating leverage. Suppose
for all the three plants Q = 40,000
Thus, a 1% increase in sales volume results in a 6% increase in profit at firm- I, a 4% profit at firm-II, and 3% profit at firm-III. This means firm-I’s
profits are more sensitive to changes in sales volume than firm-II and firm-III and firm-II’s profits are more sensitive to changes in sales volume than firm-III.
profits are more sensitive to changes in sales volume than firm-II and firm-III and firm-II’s profits are more sensitive to changes in sales volume than firm-III.