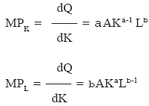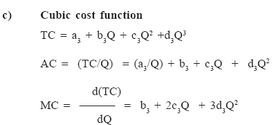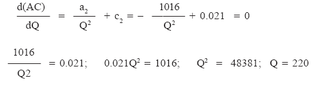INTRODUCTION
In the process of decision-making, a manager should understand clearly the relationship between the inputs and output on one hand and output and costs on the other. The short run production estimates are helpful to production managers in arriving at the optimal mix of inputs to achieve a particular output
target of a firm. This is referred to as the ‘least cost combination of inputs’ in production analysis. Also, for a given cost, optimum level of output can be
found if the production function of a firm is known. Estimation of the long run production function may help a manager in understanding and taking decisions of long term nature such as capital expenditure. Estimation of cost curves will help production manager in understanding the nature and shape of cost curves and taking useful decisions. Both short run cost function and the long run cost function must be estimated, since both sets of information will be required for some vital decisions. Knowledge of the short run cost functions allows the decision makers to judge the optimality of present output levels and to solve decision problems of production manager.Knowledge of long run cost functions is important when considering the expansion or contraction of plant size, and for confirming that the present plant size is optimal for the output level that is being produced. In the present Unit, we will discuss different approaches to examination of production and cost functions, analysis of some empirical estimates of thesefunctions, and managerial uses of the estimated functions.
ESTIMATION OF PRODUCTION FUNCTION
The principles of production theory discussed in Unit 7 are fundamental in understanding economics and provide an important conceptual framework for
analysing managerial problems. However, short run output decisions and long run planning often require more than just this conceptual framework. That is, quantitative estimates of the parameters of the production functions are required for some decisions.Functional Forms of Production Function
The production function can be estimated by regression techniques (refer to MS-8, course on “Quantitative Analysis for Managerial Applications” to know
about regression techniques) using historical data (either time-series data, or cross-section data, or engineering data). For this, one of the first tasks is to select a functional form, that is, the specific relationship among the relevant economic variables. We know that the general form of production function is, Q = f (K,L) Where, Q = output, K = capital and L = labour. Although, a variety of functional forms have been used to describe production relationships, only the Cobb-Douglas production function is discussed here. The general form of Cobb-Douglas function is expressed as: Q = AKa Lb where A, a, and b are the constants that, when estimated, describe the quantitative relationship between the inputs (K and L) and output (Q). The marginal products of capital and labour and the rates of the capital and labour inputs are functions of the constants A, a, and b and. That is,
In the process of decision-making, a manager should understand clearly the relationship between the inputs and output on one hand and output and costs on the other. The short run production estimates are helpful to production managers in arriving at the optimal mix of inputs to achieve a particular output
target of a firm. This is referred to as the ‘least cost combination of inputs’ in production analysis. Also, for a given cost, optimum level of output can be
found if the production function of a firm is known. Estimation of the long run production function may help a manager in understanding and taking decisions of long term nature such as capital expenditure. Estimation of cost curves will help production manager in understanding the nature and shape of cost curves and taking useful decisions. Both short run cost function and the long run cost function must be estimated, since both sets of information will be required for some vital decisions. Knowledge of the short run cost functions allows the decision makers to judge the optimality of present output levels and to solve decision problems of production manager.Knowledge of long run cost functions is important when considering the expansion or contraction of plant size, and for confirming that the present plant size is optimal for the output level that is being produced. In the present Unit, we will discuss different approaches to examination of production and cost functions, analysis of some empirical estimates of thesefunctions, and managerial uses of the estimated functions.
ESTIMATION OF PRODUCTION FUNCTION
The principles of production theory discussed in Unit 7 are fundamental in understanding economics and provide an important conceptual framework for
analysing managerial problems. However, short run output decisions and long run planning often require more than just this conceptual framework. That is, quantitative estimates of the parameters of the production functions are required for some decisions.Functional Forms of Production Function
The production function can be estimated by regression techniques (refer to MS-8, course on “Quantitative Analysis for Managerial Applications” to know
about regression techniques) using historical data (either time-series data, or cross-section data, or engineering data). For this, one of the first tasks is to select a functional form, that is, the specific relationship among the relevant economic variables. We know that the general form of production function is, Q = f (K,L) Where, Q = output, K = capital and L = labour. Although, a variety of functional forms have been used to describe production relationships, only the Cobb-Douglas production function is discussed here. The general form of Cobb-Douglas function is expressed as: Q = AKa Lb where A, a, and b are the constants that, when estimated, describe the quantitative relationship between the inputs (K and L) and output (Q). The marginal products of capital and labour and the rates of the capital and labour inputs are functions of the constants A, a, and b and. That is,
The sum of the constants (a+b) can be used to determine returns to scale. That is,
(a+b) > 1 Þ increasing returns to scale,
(a+b) = 1 Þ constant returns to scale, and
(a+b) < 1 Þ decreasing returns to scale.
Having numerical estimates for the constants of the production function provides significant information about the production system under study. The
marginal products for each input and returns to scale can all be determined from the estimated function. The Cobb-Douglas function does not lend itself directly to estimation by the regression methods because it is a nonlinear relationship. Technically, an equation must be a linear function of the parameters in order to use the ordinary least-squares regression method of estimation. However, a linear equation can be derived by taking the logarithm of each term. That is,
(a+b) > 1 Þ increasing returns to scale,
(a+b) = 1 Þ constant returns to scale, and
(a+b) < 1 Þ decreasing returns to scale.
Having numerical estimates for the constants of the production function provides significant information about the production system under study. The
marginal products for each input and returns to scale can all be determined from the estimated function. The Cobb-Douglas function does not lend itself directly to estimation by the regression methods because it is a nonlinear relationship. Technically, an equation must be a linear function of the parameters in order to use the ordinary least-squares regression method of estimation. However, a linear equation can be derived by taking the logarithm of each term. That is,
This function can be estimated directly by the least-squares regression technique and the estimated parameters used to determine all the important
production relationships. Then the antilogarithm of both sides can be taken, which transforms the estimated function back to its conventional multiplicative form. We will not be studying here the details of computing production function since there are a number of computer programs available for this purpose. Instead, we will provide in the following section some empirical estimates of Cobb-Douglas production function and their interpretation in the process of decision making.
Types of Statistical Analyses
Once a functional form of a production function is chosen the next step is to select the type of statistical analysis to be used in its estimation. Generally,
there are three types of statistical analyses used for estimation of a production function. These are: (a) time series analysis, (b) cross-section analysis and(c) engineering analysis.
a) Time series analysis: The amount of various inputs used in various periods in the past and the amount of output produced in each period is
called time series data. For example, we may obtain data concerning the amount of labour, the amount of capital, and the amount of various raw
materials used in the steel industry during each year from 1970 to 2000. On the basis of such data and information concerning the annual output of
steel during 1970 to 2000, we may estimate the relationship between the amounts of the inputs and the resulting output, using regression techniques.
Analysis of time series data is appropriate for a single firm that has not undergone significant changes in technology during the time span analysed.
That is, we cannot use time series data for estimating the production function of a firm that has gone through significant technological changes.
There are even more problems associated with the estimation a production function for an industry using time series data. For example, even if all
firms have operated over the same time span, changes in capacity, inputs and outputs may have proceeded at a different pace for each firm. Thus,
cross section data may be more appropriate.
b) Cross-section analysis: The amount of inputs used and output produced in various firms or sectors of the industry at a given time is called crosssection
data. For example, we may obtain data concerning the amount of labour, the amount of capital, and the amount of various raw materials used
in various firms in the steel industry in the year 2000. On the basis of such data and information concerning the year 2000, output of each firm, we may
use regression techniques to estimate the relationship between the amounts of the inputs and the resulting output.
c) Engineering analysis: In this analysis we use technical information supplied by the engineer or the agricultural scientist. This analysis is
undertaken when the above two types do not suffice. The data in this analysis is collected by experiment or from experience with day-to-dayworking of the technical process. There are advantages to be gained from and approaching the measurement of the production function from this angle because the range of applicability of the data is known, and, unlike time series and cross-section studies, we are not restricted to the narrow range of actual observations.
Limitations of Different Types of Statistical Analysis
Each of the methods discussed above has certain limitations.
1. Both time-series and cross-section analysis are restricted to a relatively narrow range of observed values. Extrapolation of the production function
outside that range may be seriously misleading. For example, in a given case, marginal productivity might decrease rapidly above 85% capacity utilization; the production function derived for values in the 70%-85% capacity utilization range would not show this.
2. Another limitation of time series analysis is the assumption that all observed values of the variables pertains to one and the same production function. In other words, a constant technology is assumed. In reality, most firms or industries, however, find better, faster, and/or cheaper ways of producing
their output. As their technology changes, they are actually creating new production functions. One way of coping with such technological changes is
to make it one of the independent variables.
3. Theoretically, the production function includes only efficient (least-cost) combinations of inputs. If measurements were to conform to this concept,
any year in which the production was less than nominal would have to be excluded from the data. It is very difficult to find a time-series data, which
satisfy technical efficiency criteria as a normal case.
4. Engineering data may overcome the limitations of time series data but mostly they concentrate on manufacturing activities. Engineering data do not tell us anything about the firm’s marketing or financial activities, even though these activities may directly affect production.
5. In addition, there are both conceptual and statistical problems in measuring data on inputs and outputs. It may be possible to measure output directly in physical units such as tons of coal, steel etc. In case more than one product is being produced, one may compute the weighted average of output, the weights being given by the cost of manufacturing these products. In a highly diversified manufacturing unit, there may be no alternative but to use the series of output values, corrected for changes in the price of products. One has also to choose between ‘gross value’ and ‘net value’. It seems better to use “net value added” concept instead of output concept in estimating production function, particularly where raw-material intensity is high. The data on labour is mostly available in the form of “number of workers employed” or “hours of labour employed”. The ‘number of workers’ data should not be used because, it may not reflect underemployment of labour, and they may be occupied, but not productively employed. Even if we use ‘man\ hours’ data, it should be adjusted for efficiency factor. It is also not advisable that labour should be measured in monetary terms as given by expenditure on
wages, bonus, etc. The data on capital input has always posed serious problems. Net investment i.e. a change in the value of capital stock, is considered most appropriate. Nevertheless, there are problems of measuring depreciation in fixed capital, changes in quality of fixed capital, changes in inventory valuation, changes in composition and productivity of working capital, etc. Finally, when one attempts an econometric estimate of a production function,
one has to overcome the standard problem of multi-collinearity among inputs,autocorrelation, homoscadasticity, etc.
EMPIRICAL ESTIMATES OF PRODUCTION FUNCTION
Consider the following Cobb-Douglas production function with parametersA=1.01, a = 0.25 and b=0.75,Q = 1.01K0.25 L0.75
The above production function can be used to estimate the required capital andlabour for various levels of output.
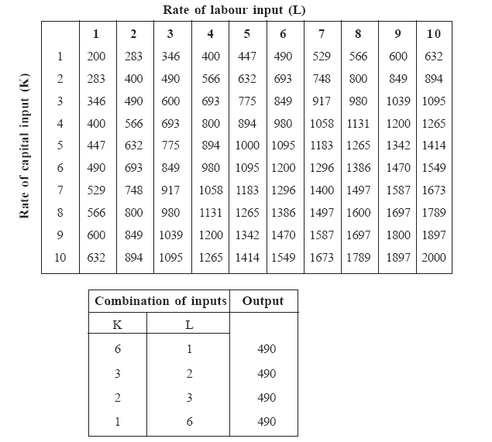
For example, the capital and labourrequired for an output level of 100 units will be given by100 = 1.01K0.25 L0.75Þ 99 = K0.25 L0.75By substituting any value of L (or K) in this equation, we can obtain theassociated value of K (or L). For example, if L=50, the value of K will begiven by99 = K0.25 (50)0.75Þ log 99 = 0.75 log 50 + 0.25 log KÞ 1.9956 = 0.75 (1.6990) + 0.25 log K1Þ log K = —— (1.9956 – 1.2743) = 2.88520.25Þ K = antilog 2.8852 = 768Similarly, for any given value of K we can find out the corresponding value ofL.As explained in Unit 7, an isoquant for any given output level or an isoquantmap for a given set of output levels can be derived from an estimatedproduction function.Consider the following Cobb-Douglas production function with parametersA=200, a = 0.50 and b = 0.50,Q = 200K0.50 L0.50For different combinations of inputs (L and K), we can construct an associatedmaximum rate of output as given in Table 10.1 For example, if two units oflabour and 9 units of capital are used, maximum production is 600 units ofoutput. If K=10 and L=10 the output rate will be 2000. The following threeimportant relationships are shown by the data in this production Table.. Table 1 indicates that there are a variety of ways to produce a particularrate of output.
For example, 490 units of output can be produced with anyone of the following combinations of inputs.
production relationships. Then the antilogarithm of both sides can be taken, which transforms the estimated function back to its conventional multiplicative form. We will not be studying here the details of computing production function since there are a number of computer programs available for this purpose. Instead, we will provide in the following section some empirical estimates of Cobb-Douglas production function and their interpretation in the process of decision making.
Types of Statistical Analyses
Once a functional form of a production function is chosen the next step is to select the type of statistical analysis to be used in its estimation. Generally,
there are three types of statistical analyses used for estimation of a production function. These are: (a) time series analysis, (b) cross-section analysis and(c) engineering analysis.
a) Time series analysis: The amount of various inputs used in various periods in the past and the amount of output produced in each period is
called time series data. For example, we may obtain data concerning the amount of labour, the amount of capital, and the amount of various raw
materials used in the steel industry during each year from 1970 to 2000. On the basis of such data and information concerning the annual output of
steel during 1970 to 2000, we may estimate the relationship between the amounts of the inputs and the resulting output, using regression techniques.
Analysis of time series data is appropriate for a single firm that has not undergone significant changes in technology during the time span analysed.
That is, we cannot use time series data for estimating the production function of a firm that has gone through significant technological changes.
There are even more problems associated with the estimation a production function for an industry using time series data. For example, even if all
firms have operated over the same time span, changes in capacity, inputs and outputs may have proceeded at a different pace for each firm. Thus,
cross section data may be more appropriate.
b) Cross-section analysis: The amount of inputs used and output produced in various firms or sectors of the industry at a given time is called crosssection
data. For example, we may obtain data concerning the amount of labour, the amount of capital, and the amount of various raw materials used
in various firms in the steel industry in the year 2000. On the basis of such data and information concerning the year 2000, output of each firm, we may
use regression techniques to estimate the relationship between the amounts of the inputs and the resulting output.
c) Engineering analysis: In this analysis we use technical information supplied by the engineer or the agricultural scientist. This analysis is
undertaken when the above two types do not suffice. The data in this analysis is collected by experiment or from experience with day-to-dayworking of the technical process. There are advantages to be gained from and approaching the measurement of the production function from this angle because the range of applicability of the data is known, and, unlike time series and cross-section studies, we are not restricted to the narrow range of actual observations.
Limitations of Different Types of Statistical Analysis
Each of the methods discussed above has certain limitations.
1. Both time-series and cross-section analysis are restricted to a relatively narrow range of observed values. Extrapolation of the production function
outside that range may be seriously misleading. For example, in a given case, marginal productivity might decrease rapidly above 85% capacity utilization; the production function derived for values in the 70%-85% capacity utilization range would not show this.
2. Another limitation of time series analysis is the assumption that all observed values of the variables pertains to one and the same production function. In other words, a constant technology is assumed. In reality, most firms or industries, however, find better, faster, and/or cheaper ways of producing
their output. As their technology changes, they are actually creating new production functions. One way of coping with such technological changes is
to make it one of the independent variables.
3. Theoretically, the production function includes only efficient (least-cost) combinations of inputs. If measurements were to conform to this concept,
any year in which the production was less than nominal would have to be excluded from the data. It is very difficult to find a time-series data, which
satisfy technical efficiency criteria as a normal case.
4. Engineering data may overcome the limitations of time series data but mostly they concentrate on manufacturing activities. Engineering data do not tell us anything about the firm’s marketing or financial activities, even though these activities may directly affect production.
5. In addition, there are both conceptual and statistical problems in measuring data on inputs and outputs. It may be possible to measure output directly in physical units such as tons of coal, steel etc. In case more than one product is being produced, one may compute the weighted average of output, the weights being given by the cost of manufacturing these products. In a highly diversified manufacturing unit, there may be no alternative but to use the series of output values, corrected for changes in the price of products. One has also to choose between ‘gross value’ and ‘net value’. It seems better to use “net value added” concept instead of output concept in estimating production function, particularly where raw-material intensity is high. The data on labour is mostly available in the form of “number of workers employed” or “hours of labour employed”. The ‘number of workers’ data should not be used because, it may not reflect underemployment of labour, and they may be occupied, but not productively employed. Even if we use ‘man\ hours’ data, it should be adjusted for efficiency factor. It is also not advisable that labour should be measured in monetary terms as given by expenditure on
wages, bonus, etc. The data on capital input has always posed serious problems. Net investment i.e. a change in the value of capital stock, is considered most appropriate. Nevertheless, there are problems of measuring depreciation in fixed capital, changes in quality of fixed capital, changes in inventory valuation, changes in composition and productivity of working capital, etc. Finally, when one attempts an econometric estimate of a production function,
one has to overcome the standard problem of multi-collinearity among inputs,autocorrelation, homoscadasticity, etc.
EMPIRICAL ESTIMATES OF PRODUCTION FUNCTION
Consider the following Cobb-Douglas production function with parametersA=1.01, a = 0.25 and b=0.75,Q = 1.01K0.25 L0.75
The above production function can be used to estimate the required capital andlabour for various levels of output.
For example, the capital and labourrequired for an output level of 100 units will be given by100 = 1.01K0.25 L0.75Þ 99 = K0.25 L0.75By substituting any value of L (or K) in this equation, we can obtain theassociated value of K (or L). For example, if L=50, the value of K will begiven by99 = K0.25 (50)0.75Þ log 99 = 0.75 log 50 + 0.25 log KÞ 1.9956 = 0.75 (1.6990) + 0.25 log K1Þ log K = —— (1.9956 – 1.2743) = 2.88520.25Þ K = antilog 2.8852 = 768Similarly, for any given value of K we can find out the corresponding value ofL.As explained in Unit 7, an isoquant for any given output level or an isoquantmap for a given set of output levels can be derived from an estimatedproduction function.Consider the following Cobb-Douglas production function with parametersA=200, a = 0.50 and b = 0.50,Q = 200K0.50 L0.50For different combinations of inputs (L and K), we can construct an associatedmaximum rate of output as given in Table 10.1 For example, if two units oflabour and 9 units of capital are used, maximum production is 600 units ofoutput. If K=10 and L=10 the output rate will be 2000. The following threeimportant relationships are shown by the data in this production Table.. Table 1 indicates that there are a variety of ways to produce a particularrate of output.
For example, 490 units of output can be produced with anyone of the following combinations of inputs.
This shows that there is substitutability between the factors of production. That means the production manager can use either the input combination
(k=6 and L=1) or (k=3 and L=2) or (k=2 and L=3) or (k=1 and L=6) to produce the same amount of output (490 units). The concept of substitution
is important because it means that managers can change the input mix of capital and labour in response to changes in the relative prices of these inputs.
2. In the equation given that a = 0.50 and b = 0.50. The sum of these constants is 1 (0.50+0.50=1). This indicates that there are constant returns
to scale (a+b=1). This means that a 1% increase in all inputs would result in a 1% increase in output. For example, in Table 10.1 maximum production
with four units of capital and one unit of labour is 400. Doubling the input rates to K=8 and L=2 results in the rate of output doubling to Q=800. In
Table 10.1, production is characterized by constant returns to scale. This means that if both input rates increase by the same factor (for example,
both input rates double), the rate of output also will double. In other production functions, output may increase more or less than in proportion to
changes in inputs. In contrast to the concept of returns to scale, when output changes because of changes in one input while the other remains constant, the changes in the output rates are referred to as returns to a factor. In Table , if the rate of one input is held constant while the other is increased, output increases but the successive increments become smaller. For example, from Table it can be seen that if the rate of capital is held constant at K=2 and labour is increased from L=1 to L=6, the successive increases in output are 117, 90, 76, 67, and 60. As discussed in Unit 7, this relationship is known
as diminishing marginal returns.We will consider another empirical estimate of Cobb-Douglas production function given as: Q = 10.2K0.194 L0.878
Here, the returns to scale are increasing because a+b=1.072 is greater than 1. The marginal product functions for capital and labour are MPK = aAKa-1Lb = 0.194(10.2)K(0.194-1)L0.878 = 0.194(10.2)K-0.806L0.878 and MPL = bAKaLb-1 = 0.878(10.2)K0.194L(0.878-1) = 0.878(10.2)K0.194L-0.122 Based on the above MPK and MPL equations we can calculate marginal products of capital and labour for a given input combination. For example, suppose we are given that the input combination K=20 and L=30. Substituting these values for the constants A, a, and b gives the following marginal products: MPK = 0.194(10.2)(20)-0.806(30)0.878 = 3.50 and MPL = 0.878(10.2)(20)0.194 (30)-0.122 = 10.58 We can interpret the above marginal products of capital and labour as follows. One unit change in capital with labour held constant at 30 would result in 3.50 unit change in output, and one unit change in labour with capital held constant at 20 would be associated with a 10.58 unit change in output. Empirical estimates of production functions for industries such as sugar, textiles, cement etc., are available in the Indian context. We will briefly discuss some of these empirical estimates here. There are many empirical studies of production functions in different countries.John R. Moroney made one comprehensive study of a number of manufacturing industries in U.S.A. He estimated the production function:
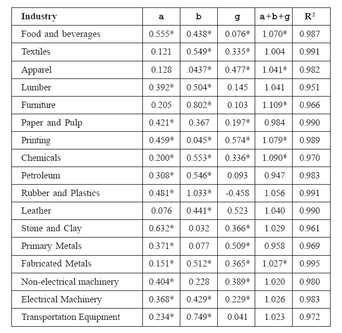
Q = AKa L1/bL2g
Where, K = value of capital
L1 = production worker-hours
L2 = non-production worker-hours
A summary of the estimated values of the production elasticities (a, b, and g) and R2, the coefficient of determination, for each industry is shown in Table From Table it can be observed that R2 values are very high (more than 0.951) for all the functions. This means that more than 95% of the variation in output is explained by variation in the three inputs. A test of significance was made for each estimated parameter, a, b, and g, using the standard t-test. Those estimated production elasticities that are statistically significant at the 0.05 levels are indicated with an asterix (*). The sum of the estimated
production elasticities (a+b+g) provides a point estimate of returns to scale in each industry. Although, the sum exceeds unity in 14 of the 17 industries, it is statistically significant only in the following industries: food and beverages, apparel, furniture, printing, chemicals, and fabricated metals. Thus, only in
those six industries there are increasing returns to scale. For example, in the fabricated metals industry, a 1% increase in all inputs is estimated to result in a 1.027% increase in output.
(k=6 and L=1) or (k=3 and L=2) or (k=2 and L=3) or (k=1 and L=6) to produce the same amount of output (490 units). The concept of substitution
is important because it means that managers can change the input mix of capital and labour in response to changes in the relative prices of these inputs.
2. In the equation given that a = 0.50 and b = 0.50. The sum of these constants is 1 (0.50+0.50=1). This indicates that there are constant returns
to scale (a+b=1). This means that a 1% increase in all inputs would result in a 1% increase in output. For example, in Table 10.1 maximum production
with four units of capital and one unit of labour is 400. Doubling the input rates to K=8 and L=2 results in the rate of output doubling to Q=800. In
Table 10.1, production is characterized by constant returns to scale. This means that if both input rates increase by the same factor (for example,
both input rates double), the rate of output also will double. In other production functions, output may increase more or less than in proportion to
changes in inputs. In contrast to the concept of returns to scale, when output changes because of changes in one input while the other remains constant, the changes in the output rates are referred to as returns to a factor. In Table , if the rate of one input is held constant while the other is increased, output increases but the successive increments become smaller. For example, from Table it can be seen that if the rate of capital is held constant at K=2 and labour is increased from L=1 to L=6, the successive increases in output are 117, 90, 76, 67, and 60. As discussed in Unit 7, this relationship is known
as diminishing marginal returns.We will consider another empirical estimate of Cobb-Douglas production function given as: Q = 10.2K0.194 L0.878
Here, the returns to scale are increasing because a+b=1.072 is greater than 1. The marginal product functions for capital and labour are MPK = aAKa-1Lb = 0.194(10.2)K(0.194-1)L0.878 = 0.194(10.2)K-0.806L0.878 and MPL = bAKaLb-1 = 0.878(10.2)K0.194L(0.878-1) = 0.878(10.2)K0.194L-0.122 Based on the above MPK and MPL equations we can calculate marginal products of capital and labour for a given input combination. For example, suppose we are given that the input combination K=20 and L=30. Substituting these values for the constants A, a, and b gives the following marginal products: MPK = 0.194(10.2)(20)-0.806(30)0.878 = 3.50 and MPL = 0.878(10.2)(20)0.194 (30)-0.122 = 10.58 We can interpret the above marginal products of capital and labour as follows. One unit change in capital with labour held constant at 30 would result in 3.50 unit change in output, and one unit change in labour with capital held constant at 20 would be associated with a 10.58 unit change in output. Empirical estimates of production functions for industries such as sugar, textiles, cement etc., are available in the Indian context. We will briefly discuss some of these empirical estimates here. There are many empirical studies of production functions in different countries.John R. Moroney made one comprehensive study of a number of manufacturing industries in U.S.A. He estimated the production function:
Q = AKa L1/bL2g
Where, K = value of capital
L1 = production worker-hours
L2 = non-production worker-hours
A summary of the estimated values of the production elasticities (a, b, and g) and R2, the coefficient of determination, for each industry is shown in Table From Table it can be observed that R2 values are very high (more than 0.951) for all the functions. This means that more than 95% of the variation in output is explained by variation in the three inputs. A test of significance was made for each estimated parameter, a, b, and g, using the standard t-test. Those estimated production elasticities that are statistically significant at the 0.05 levels are indicated with an asterix (*). The sum of the estimated
production elasticities (a+b+g) provides a point estimate of returns to scale in each industry. Although, the sum exceeds unity in 14 of the 17 industries, it is statistically significant only in the following industries: food and beverages, apparel, furniture, printing, chemicals, and fabricated metals. Thus, only in
those six industries there are increasing returns to scale. For example, in the fabricated metals industry, a 1% increase in all inputs is estimated to result in a 1.027% increase in output.
MANAGERIAL USES OF PRODUCTION FUNCTION
There are several managerial uses of the production function. It can be used to compute the least-cost combination of inputs for a given output or to choose the input combination that yields the maximum level of output with a given level of cost. There are several feasible combinations of input factors and it is highly useful for decision-makers to find out the most appropriate among them. The production function is useful in deciding on the additional value of employing a variable input in the production process. So long as the marginal revenue productivity of a variable factor exceeds it price, it may be worthwhile to increase its use. The additional use of an input factor should be stopped when its marginal revenue productivity just equals its price. Production functions also aid long-run decision-making. If returns to scale are increasing,it will be worthwhile to increase production through a proportionate increase in all factors of production, provided, there is enough demand for the product. On the other hand, if returns to scale are decreasing, it may not be worthwhile to increase the production through a proportionate increase in all factors of production, even if there is enough demand for the product. However, it may in the discretion of the producer to increase or decrease production in the presence of constant returns to scale, if there is enough demand for the product.
COST FUNCTION AND ITS DETERMINANTS
Cost function expresses the relationship between cost and its determinants such as the size of plant, level of output, input prices, technology, managerial
efficiency, etc. In a mathematical form, it can be expressed as, C = f (S, O, P, T, E…..) Where, C = cost (it can be unit cost or total cost) S = plant size
O = output level
P = prices of inputs used in production
T = nature of technology
E = managerial efficiency
Determinants of Cost Function
The cost of production depends on many factors and these factors vary from one firm to another firm in the same industry or from one industry to another
industry. The main determinants of a cost function are:
a) plant size
b) output level
c) prices of inputs used in production,
d) nature of technology
e) managerial efficiency
We will discuss briefly the influence of each of these factors on cost.
a) Plant size: Plant size is an important variable in determining cost. The scale of operations or plant size and the unit cost are inversely related in the
sense that as the former increases, unit cost decreases, and vice versa. Such a relationship gives downward slope of cost function depending upon
the different sizes of plants taken into account. Such a cost function gives primarily engineering estimates of cost.
b) Output level: Output level and total cost are positively related, as the total cost increases with increase in output and total cost decreases with
decrease in output. This is because increased production requires increased use of raw materials, labour, etc., and if the increase is substantial, even
fixed inputs like plant and equipment, and managerial staff may have to be increased.
c) Price of inputs: Changes in input prices also influence cost, depending on the relative usage of the inputs and relative changes in their prices. This is
because more money will have to be paid to those inputs whose prices have increased and there will be no simultaneous reduction in the costs from any
other source. Therefore, the cost of production varies directly with the prices of production.
d) Technology: Technology is a significant factor in determining cost. By definition, improvement in technology increases production leading to increase
in productivity and decrease in production cost. Therefore, cost varies inversely with technological progress. Technology is often quantified as
capital-output ratio. Improved technology is generally found to have higher capital-output ratio.
e) Managerial efficiency: This is another factor influencing the cost of
production. More the managerial efficiency less the cost of production. It is difficult to measure managerial efficiency quantitatively. However, a and change in cost at two points of time may explain how organisational or managerial changes within the firm have brought about cost efficiency, provided it is possible to exclude the effect of other factors.
ESTIMATION OF COST FUNCTION
Several methods exist for the measurement of the actual cost-output relation fora particular firm or a group of firms, but the three broad approaches -accounting, engineering and econometric - are the most important and commonly used.
Accounting Method This method is used by the cost accountants. In this method, the cost-outputrelationship is estimated by classifying the total cost into fixed, variable andsemi-variable costs. These components are then estimated separately. Theaverage variable cost, the semi-variable cost which is fixed over a certainrange of output, and fixed costs are determined on the basis of inspection and experience. The total cost, the average cost and the marginal cost for eachlevel of output can then be obtained through a simple arithmetic procedure.Although, the accounting method appears to be quite simple, it is a bitcumbersome as one has to maintain a detailed breakdown of costs over aperiod to arrive at good estimates of actual cost-output relationship. One musthave experience with a wide range of fluctuations in output rate to come upwith accurate estimates.
Engineering Method The engineering method of cost estimation is based directly on the physicalrelationship of inputs to output, and uses the price of inputs to determine costs.This method of estimating real world cost function rests clearly on theknowledge that the shape of any cost function is dependent on:(a) theproduction function and (b) the price of inputs.We have seen earlier in this Unit while discussing the estimation of productionfunction that for a given the production function and input prices, the optimuminput combination for a given output level can be determined. The resultant costcurve can then be formulated by multiplying each input in the least costcombination by its price, to develop the cost function. This method is calledengineering method as the estimates of least cost combinations are provided byengineers.The assumption made while using this method is that both the technology andfactor prices are constant. This method may not always give the correctestimate of costs as the technology and factor prices do change substantiallyover a period of time. Therefore, this method is more relevant for the shortrun. Also, this method may be useful if good historical data is difficult toobtain. But this method requires a sound understanding of engineering and adetailed sampling of the different processes under controlled conditions, whichmay not always be possible.
Econometric Method This method is also some times called statistical method and is widely used forestimating cost functions. Under this method, the historical data on cost andoutput are used to estimate the cost-output relationship. The basic techniqueof regression is used for this purpose. The data could be a time series data of a firm in the industry or of all firms in the industry or a cross-section data for a particular year from various firms in the industry. Depending on the kind of data used, we can estimate short run or long run cost functions. For instance, if time series data of a firm whose output capacity has not changed much during the sample period is used, the cost function will be short run. On the other hand, if cross-section data of many firms with varying sizes, or the time series data of the industry as a whole is used, the estimated cost function will be the long run one. The procedure for estimation of cost function involves three steps. First, the determinants of cost are identified. Second, the functional form of the cost function is specified. Third, the functional form is chosen and then the basic technique of regression is applied to estimate the chosen functional form.
Functional Forms of Cost Function The following are the three common functional forms of cost function in termsof total cost function (TC).a) Linear cost function: TC = a1 + b1Qb) Quadratic cost function: TC = a2 + b2Q + c2Q2c) Cubic cost function: TC = a3 + b3Q + c3Q2 +d3Q3Where, a1, a2, a3, b1, b2, b3, c2, c3, d3 are constants.When all the determinants of cost are chosen and the data collection iscomplete, the alternative functional forms can be estimated by using regressionsoftware package on a computer. The most appropriate form of the costfunction for decision-making is then chosen on the basis of the principles ofeconomic theory and statistical inference.Once the constants in the total cost function are estimated using regressiontechnique, the average cost (AC) and marginal cost (MC) functions for chosenforms of cost function will be calculated. The TC, AC and MC cost functionsfor different functional forms of total cost function and their typical graphicalpresentation and interpretation are explained below.
There are several managerial uses of the production function. It can be used to compute the least-cost combination of inputs for a given output or to choose the input combination that yields the maximum level of output with a given level of cost. There are several feasible combinations of input factors and it is highly useful for decision-makers to find out the most appropriate among them. The production function is useful in deciding on the additional value of employing a variable input in the production process. So long as the marginal revenue productivity of a variable factor exceeds it price, it may be worthwhile to increase its use. The additional use of an input factor should be stopped when its marginal revenue productivity just equals its price. Production functions also aid long-run decision-making. If returns to scale are increasing,it will be worthwhile to increase production through a proportionate increase in all factors of production, provided, there is enough demand for the product. On the other hand, if returns to scale are decreasing, it may not be worthwhile to increase the production through a proportionate increase in all factors of production, even if there is enough demand for the product. However, it may in the discretion of the producer to increase or decrease production in the presence of constant returns to scale, if there is enough demand for the product.
COST FUNCTION AND ITS DETERMINANTS
Cost function expresses the relationship between cost and its determinants such as the size of plant, level of output, input prices, technology, managerial
efficiency, etc. In a mathematical form, it can be expressed as, C = f (S, O, P, T, E…..) Where, C = cost (it can be unit cost or total cost) S = plant size
O = output level
P = prices of inputs used in production
T = nature of technology
E = managerial efficiency
Determinants of Cost Function
The cost of production depends on many factors and these factors vary from one firm to another firm in the same industry or from one industry to another
industry. The main determinants of a cost function are:
a) plant size
b) output level
c) prices of inputs used in production,
d) nature of technology
e) managerial efficiency
We will discuss briefly the influence of each of these factors on cost.
a) Plant size: Plant size is an important variable in determining cost. The scale of operations or plant size and the unit cost are inversely related in the
sense that as the former increases, unit cost decreases, and vice versa. Such a relationship gives downward slope of cost function depending upon
the different sizes of plants taken into account. Such a cost function gives primarily engineering estimates of cost.
b) Output level: Output level and total cost are positively related, as the total cost increases with increase in output and total cost decreases with
decrease in output. This is because increased production requires increased use of raw materials, labour, etc., and if the increase is substantial, even
fixed inputs like plant and equipment, and managerial staff may have to be increased.
c) Price of inputs: Changes in input prices also influence cost, depending on the relative usage of the inputs and relative changes in their prices. This is
because more money will have to be paid to those inputs whose prices have increased and there will be no simultaneous reduction in the costs from any
other source. Therefore, the cost of production varies directly with the prices of production.
d) Technology: Technology is a significant factor in determining cost. By definition, improvement in technology increases production leading to increase
in productivity and decrease in production cost. Therefore, cost varies inversely with technological progress. Technology is often quantified as
capital-output ratio. Improved technology is generally found to have higher capital-output ratio.
e) Managerial efficiency: This is another factor influencing the cost of
production. More the managerial efficiency less the cost of production. It is difficult to measure managerial efficiency quantitatively. However, a and change in cost at two points of time may explain how organisational or managerial changes within the firm have brought about cost efficiency, provided it is possible to exclude the effect of other factors.
ESTIMATION OF COST FUNCTION
Several methods exist for the measurement of the actual cost-output relation fora particular firm or a group of firms, but the three broad approaches -accounting, engineering and econometric - are the most important and commonly used.
Accounting Method This method is used by the cost accountants. In this method, the cost-outputrelationship is estimated by classifying the total cost into fixed, variable andsemi-variable costs. These components are then estimated separately. Theaverage variable cost, the semi-variable cost which is fixed over a certainrange of output, and fixed costs are determined on the basis of inspection and experience. The total cost, the average cost and the marginal cost for eachlevel of output can then be obtained through a simple arithmetic procedure.Although, the accounting method appears to be quite simple, it is a bitcumbersome as one has to maintain a detailed breakdown of costs over aperiod to arrive at good estimates of actual cost-output relationship. One musthave experience with a wide range of fluctuations in output rate to come upwith accurate estimates.
Engineering Method The engineering method of cost estimation is based directly on the physicalrelationship of inputs to output, and uses the price of inputs to determine costs.This method of estimating real world cost function rests clearly on theknowledge that the shape of any cost function is dependent on:(a) theproduction function and (b) the price of inputs.We have seen earlier in this Unit while discussing the estimation of productionfunction that for a given the production function and input prices, the optimuminput combination for a given output level can be determined. The resultant costcurve can then be formulated by multiplying each input in the least costcombination by its price, to develop the cost function. This method is calledengineering method as the estimates of least cost combinations are provided byengineers.The assumption made while using this method is that both the technology andfactor prices are constant. This method may not always give the correctestimate of costs as the technology and factor prices do change substantiallyover a period of time. Therefore, this method is more relevant for the shortrun. Also, this method may be useful if good historical data is difficult toobtain. But this method requires a sound understanding of engineering and adetailed sampling of the different processes under controlled conditions, whichmay not always be possible.
Econometric Method This method is also some times called statistical method and is widely used forestimating cost functions. Under this method, the historical data on cost andoutput are used to estimate the cost-output relationship. The basic techniqueof regression is used for this purpose. The data could be a time series data of a firm in the industry or of all firms in the industry or a cross-section data for a particular year from various firms in the industry. Depending on the kind of data used, we can estimate short run or long run cost functions. For instance, if time series data of a firm whose output capacity has not changed much during the sample period is used, the cost function will be short run. On the other hand, if cross-section data of many firms with varying sizes, or the time series data of the industry as a whole is used, the estimated cost function will be the long run one. The procedure for estimation of cost function involves three steps. First, the determinants of cost are identified. Second, the functional form of the cost function is specified. Third, the functional form is chosen and then the basic technique of regression is applied to estimate the chosen functional form.
Functional Forms of Cost Function The following are the three common functional forms of cost function in termsof total cost function (TC).a) Linear cost function: TC = a1 + b1Qb) Quadratic cost function: TC = a2 + b2Q + c2Q2c) Cubic cost function: TC = a3 + b3Q + c3Q2 +d3Q3Where, a1, a2, a3, b1, b2, b3, c2, c3, d3 are constants.When all the determinants of cost are chosen and the data collection iscomplete, the alternative functional forms can be estimated by using regressionsoftware package on a computer. The most appropriate form of the costfunction for decision-making is then chosen on the basis of the principles ofeconomic theory and statistical inference.Once the constants in the total cost function are estimated using regressiontechnique, the average cost (AC) and marginal cost (MC) functions for chosenforms of cost function will be calculated. The TC, AC and MC cost functionsfor different functional forms of total cost function and their typical graphicalpresentation and interpretation are explained below.
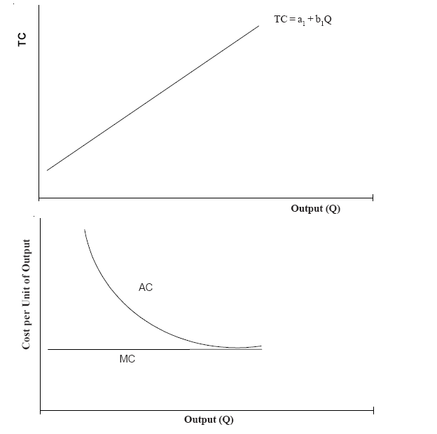
The typical TC, AC, and MC curves that are based on a linear cost function are shown in Figure. These cost functions have the following properties:
TC is a linear function, where AC declines initially and then becomes quite flat approaching the value of MC as output increases and MC is constant at b1.
TC is a linear function, where AC declines initially and then becomes quite flat approaching the value of MC as output increases and MC is constant at b1.
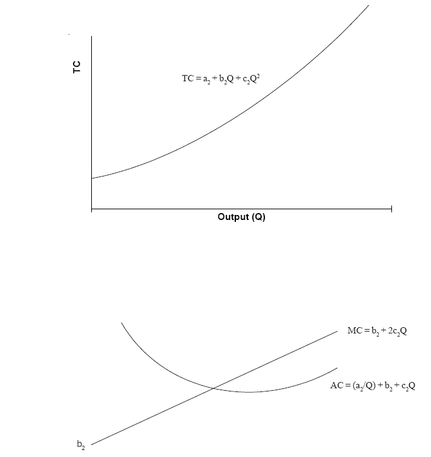
The typical TC, AC, and MC curves that are based on a quadratic cost function are shown in Figure . These cost functions have the following
properties: TC increases at an increasing rate; MC is a linearly increasing function of output; and AC is a U shaped curve.
properties: TC increases at an increasing rate; MC is a linearly increasing function of output; and AC is a U shaped curve.
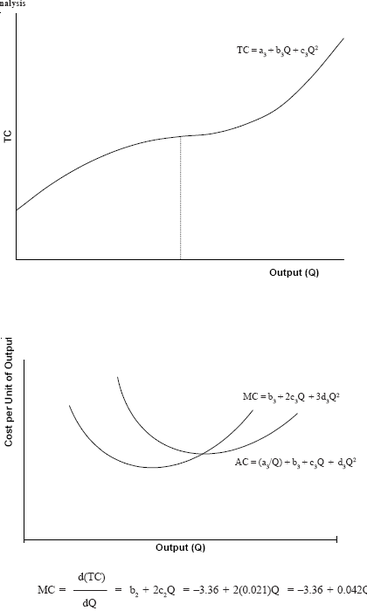
The typical TC, AC, and MC curves that are based on a cubic cost function are shown in Figure. These cost functions have the following properties:
TC first increases at a decreasing rate up to output rate Q1 in the Figure and then increases at an increasing rate; and both AC and MC cost functions
are U shaped functions. The linear total cost function would give a constant marginal cost and a monotonically falling average cost curve. The quadratic function could yield a U-shaped average cost curve but it would imply a monotonically rising marginal cost curve. The cubic cost function is consistent both with a U-shaped average cost curve and a U-shaped marginal cost curve. Thus, to check the validity of the theoretical cost-output relationship, one should hypothesize a cubic cost function.
TC first increases at a decreasing rate up to output rate Q1 in the Figure and then increases at an increasing rate; and both AC and MC cost functions
are U shaped functions. The linear total cost function would give a constant marginal cost and a monotonically falling average cost curve. The quadratic function could yield a U-shaped average cost curve but it would imply a monotonically rising marginal cost curve. The cubic cost function is consistent both with a U-shaped average cost curve and a U-shaped marginal cost curve. Thus, to check the validity of the theoretical cost-output relationship, one should hypothesize a cubic cost function.
An example of using estimated cost function: Using the output-cost data of a chemical firm, the following total cost function was estimated using quadratic function: TC = 1016 – 3.36Q + 0.021Q2
a) Determine average and marginal cost functions.
b) Determine the output rate that will minimize average cost and the per unit cost at that rate of output.
c) The firm proposed a new plant to produce nitrogen. The current market price of this fertilizer is Rs 5.50 per unit of output and is expected to remain
at that level for the foreseeable future. Should the plant be built?
i) The average cost function is AC = (TC/Q) = (a2/Q) + b2 + c2Q
a) Determine average and marginal cost functions.
b) Determine the output rate that will minimize average cost and the per unit cost at that rate of output.
c) The firm proposed a new plant to produce nitrogen. The current market price of this fertilizer is Rs 5.50 per unit of output and is expected to remain
at that level for the foreseeable future. Should the plant be built?
i) The average cost function is AC = (TC/Q) = (a2/Q) + b2 + c2Q
ii) The output rate that results in minimum per unit cost is found by taking the first derivative of the average cost function, setting it equal to zero,
and solving for Q.
and solving for Q.
To find the cost at this rate of output, substitute 220 for Q in AC equation and solve it. AC = (1016/Q) – 3.36 + 0.021Q = (1016/220) – 3.36 + (0.021 * 220)
Rs. 5.88 per unit of output.
iii) Because the lowest possible cost is Rs. 5.88 per unit, which is Rs. 0.38 above the market price (Rs. 5.50), the plant should not be constructed.
Short Run and Long Run Cost Function Estimation
The same sorts of regression techniques can be used to estimate short run cost functions and long run cost functions. However, it is very difficult to find
cases where the scale of a firm has changed but technology and other relevant factors have remained constant. Thus, it is hard to use time series data to
estimate long run cost functions. Generally, regression analysis based on cross section data has been used instead. Specially, a sample of firms of various
sizes is chosen, and a firm's TC is regressed on its output, as well as other independent variables, such as regional differences in wage rates or other input prices.
Rs. 5.88 per unit of output.
iii) Because the lowest possible cost is Rs. 5.88 per unit, which is Rs. 0.38 above the market price (Rs. 5.50), the plant should not be constructed.
Short Run and Long Run Cost Function Estimation
The same sorts of regression techniques can be used to estimate short run cost functions and long run cost functions. However, it is very difficult to find
cases where the scale of a firm has changed but technology and other relevant factors have remained constant. Thus, it is hard to use time series data to
estimate long run cost functions. Generally, regression analysis based on cross section data has been used instead. Specially, a sample of firms of various
sizes is chosen, and a firm's TC is regressed on its output, as well as other independent variables, such as regional differences in wage rates or other input prices.
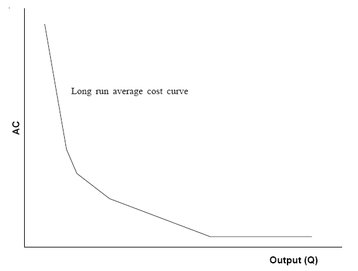
Many studies of long run cost functions that have been carried out found that there are very significant economies of scale at low output levels, but that
these economies of scale tend to diminish as output increases, and that the long run average cost function eventually becomes close to horizontal axis at high output levels. Therefore, in contrast to the U-shaped curve in Figure shown in previous unit, which is often postulated in micro economic theory, the long run average cost curve tends to be L-shaped, as shown in Figure .
Problems in Estimation of Cost Function
We confront certain problems while attempting to derive empirical costfunctions from economic data. Some of these problems are briefly discussedbelow.Long run average cost curveProduction andCost Analysis181. In collecting cost and output data we must be certain that they areproperly paired. That is, the cost data applicable to the corresponding dataon output.2. We must also try to obtain data on cost and output during a time periodwhen the output has been produced at relatively even rate. If forexample, a month is chosen as the relevant time period over which thevariables are measured, it would not be desirable to have wide weeklyfluctuations in the rate of output. The monthly data in such a casewould represent an average output rate that could disguise the true costoutputrelationship. Not only should the output rate be uniform, but italso should be a rate to which the firm is fully adjusted. Furthermore,there should be no disruptions in the output due to external factors suchas power failures, delays in receiving necessary supplies, etc. Togenerate the data necessary for a meaningful statistical analysis, theobservations must include a wide range of rates of output. Observingcost-output data for the last 24 months, when the rate of output was thesame each month, would provide little information concerning theappropriate cost function.3. The cost data is normally collected and recorded by accountants for theirown purposes and in a manner that it makes the information less thanperfect from the perspective of economic analysis. While collectinghistorical data on cost, care must be taken to ensure that all explicit aswell as implicit costs have been properly taken into account, and that allthe costs are properly identified by time period in which they wereincurred.4. For situations in which more than one product is being produced with givenproductive factors, it may not be possible to separate costs according tooutput in a meaningful way. One simple approach of allocating costsamong various products is based on the relative proportion of each productin the total output. However, this may not always accurately reflect thecost appropriate to each output.5. Since prices change over time, any money value cost would therefore relatepartly to output changes and partly to price changes. In order to estimatethe cost-output relationship, the impact of price change on cost needs to beeliminated by deflating the cost data by price indices. Wages and equipmentprice indices are readily available and frequently used to ‘deflate’ the moneycost.6. Finally, there is a problem of choosing the functional form of equation orcurve that would fit the data best. The usefulness of any cost function forpractical application depends, to a large extent, on appropriateness of thefunctional form chosen. There are three functional forms of cost functions,which are popular, viz., linear, quadratic and cubic. The choice of aparticular function depends upon the correspondence of the economicproperties of the data to the mathematical properties of the alternativehypotheses of total cost function.The accounting and engineering methods are more appropriate than theeconometric method for estimating the cost function at the firm level, while theeconometric method is more suitable for estimating the cost function at theindustry or national level. There has been a growing application of theeconometric method at the macro level and there are good prospects for its useeven at the micro level. However, it must be understood that the threeapproaches discussed above are not competitive, but are rather complementaryto each other. They supplement each other. The choice of a method thereforedepends upon the purpose of study, time and expense considerations.
EMPIRICAL ESTIMATES OF COST FUNCTION
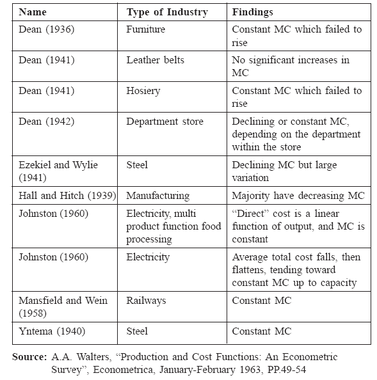
A number of studies using time series and cross-section data have beenconducted to estimate short run and long run cost behaviour of variousindustries. Table 10.3 lists a number of well-known studies estimating short runaverage and marginal cost curves. These and many other studies point oneconclusion: in the short run a linear total variable cost function with constantmarginal cost is the relationship that appears to describe best the actual costconditions over the “normal” range of production. U-shaped average cost(AC) and marginal cost (MC) curves have been found, but are less prevalentthan one might expect.
these economies of scale tend to diminish as output increases, and that the long run average cost function eventually becomes close to horizontal axis at high output levels. Therefore, in contrast to the U-shaped curve in Figure shown in previous unit, which is often postulated in micro economic theory, the long run average cost curve tends to be L-shaped, as shown in Figure .
Problems in Estimation of Cost Function
We confront certain problems while attempting to derive empirical costfunctions from economic data. Some of these problems are briefly discussedbelow.Long run average cost curveProduction andCost Analysis181. In collecting cost and output data we must be certain that they areproperly paired. That is, the cost data applicable to the corresponding dataon output.2. We must also try to obtain data on cost and output during a time periodwhen the output has been produced at relatively even rate. If forexample, a month is chosen as the relevant time period over which thevariables are measured, it would not be desirable to have wide weeklyfluctuations in the rate of output. The monthly data in such a casewould represent an average output rate that could disguise the true costoutputrelationship. Not only should the output rate be uniform, but italso should be a rate to which the firm is fully adjusted. Furthermore,there should be no disruptions in the output due to external factors suchas power failures, delays in receiving necessary supplies, etc. Togenerate the data necessary for a meaningful statistical analysis, theobservations must include a wide range of rates of output. Observingcost-output data for the last 24 months, when the rate of output was thesame each month, would provide little information concerning theappropriate cost function.3. The cost data is normally collected and recorded by accountants for theirown purposes and in a manner that it makes the information less thanperfect from the perspective of economic analysis. While collectinghistorical data on cost, care must be taken to ensure that all explicit aswell as implicit costs have been properly taken into account, and that allthe costs are properly identified by time period in which they wereincurred.4. For situations in which more than one product is being produced with givenproductive factors, it may not be possible to separate costs according tooutput in a meaningful way. One simple approach of allocating costsamong various products is based on the relative proportion of each productin the total output. However, this may not always accurately reflect thecost appropriate to each output.5. Since prices change over time, any money value cost would therefore relatepartly to output changes and partly to price changes. In order to estimatethe cost-output relationship, the impact of price change on cost needs to beeliminated by deflating the cost data by price indices. Wages and equipmentprice indices are readily available and frequently used to ‘deflate’ the moneycost.6. Finally, there is a problem of choosing the functional form of equation orcurve that would fit the data best. The usefulness of any cost function forpractical application depends, to a large extent, on appropriateness of thefunctional form chosen. There are three functional forms of cost functions,which are popular, viz., linear, quadratic and cubic. The choice of aparticular function depends upon the correspondence of the economicproperties of the data to the mathematical properties of the alternativehypotheses of total cost function.The accounting and engineering methods are more appropriate than theeconometric method for estimating the cost function at the firm level, while theeconometric method is more suitable for estimating the cost function at theindustry or national level. There has been a growing application of theeconometric method at the macro level and there are good prospects for its useeven at the micro level. However, it must be understood that the threeapproaches discussed above are not competitive, but are rather complementaryto each other. They supplement each other. The choice of a method thereforedepends upon the purpose of study, time and expense considerations.
EMPIRICAL ESTIMATES OF COST FUNCTION
A number of studies using time series and cross-section data have beenconducted to estimate short run and long run cost behaviour of variousindustries. Table 10.3 lists a number of well-known studies estimating short runaverage and marginal cost curves. These and many other studies point oneconclusion: in the short run a linear total variable cost function with constantmarginal cost is the relationship that appears to describe best the actual costconditions over the “normal” range of production. U-shaped average cost(AC) and marginal cost (MC) curves have been found, but are less prevalentthan one might expect.
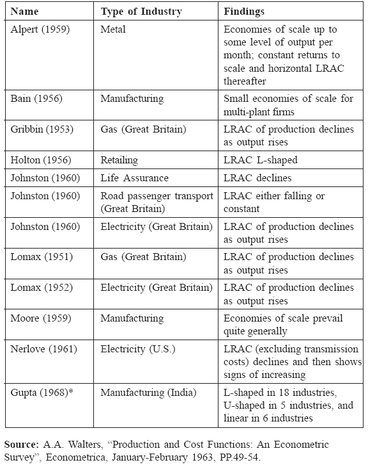
Table lists a number of well known, long run average cost studies. In some industries, such as light manufacturing (of baking products), economies of
size are relatively unimportant and diseconomies set in rather quickly, implying that a small plant has cost advantages over a large plant. In other industries, such as meat packing or the production of household appliances, the long run average cost curve is found to be flat over an extended range of output, there by indicating that a variety of different plant sizes are all more or less equally efficient. In some other industries such as electricity or metal (aluminum and steel) production, substantial economies of size are found, thereby implying that a large plant is most efficient. Rarely are substantial diseconomies of size found in empirical studies, perhaps because of firms recognising that production beyond a certain range leads to sharply rising costs. Therefore, they avoid such situations if all possible by building additional plants.
size are relatively unimportant and diseconomies set in rather quickly, implying that a small plant has cost advantages over a large plant. In other industries, such as meat packing or the production of household appliances, the long run average cost curve is found to be flat over an extended range of output, there by indicating that a variety of different plant sizes are all more or less equally efficient. In some other industries such as electricity or metal (aluminum and steel) production, substantial economies of size are found, thereby implying that a large plant is most efficient. Rarely are substantial diseconomies of size found in empirical studies, perhaps because of firms recognising that production beyond a certain range leads to sharply rising costs. Therefore, they avoid such situations if all possible by building additional plants.
MANAGERIAL USES OF COST FUNCTION
In Unit we have already discussed some of the uses and applications of cost analysis in the production process of managerial decision-making. The estimated cost function can help managers to take meaningful decisions with regard to:
1. determination of optimum plant size,
2. determination of optimum output for a given plant, and
3. determination of a firm’s supply curve.
The optimum plant size, as discussed earlier, is defined in terms of minimum costs per unit of output. In other words, an optimum plant is given by that
value of K (plant size) for which the average cost is minimum. If the long run total cost curve is a cubic function, the resultant long run average cost curve
will be a conventional U-shaped curve. The plant level at which the long run average cost is minimum will be of optimum size. For a given plant, the optimum output level will be achieved at a point where the average cost is the least. This condition can be easily verified from the short run total cost function. The level of output that a firm would like to supply to the market will depend on the price that can charge for its product. In other words, a firm’s supply is a positive function of the product price. To get the firm’s supply schedule, oneneeds to know the firm's cost function and its objectives.
In Unit we have already discussed some of the uses and applications of cost analysis in the production process of managerial decision-making. The estimated cost function can help managers to take meaningful decisions with regard to:
1. determination of optimum plant size,
2. determination of optimum output for a given plant, and
3. determination of a firm’s supply curve.
The optimum plant size, as discussed earlier, is defined in terms of minimum costs per unit of output. In other words, an optimum plant is given by that
value of K (plant size) for which the average cost is minimum. If the long run total cost curve is a cubic function, the resultant long run average cost curve
will be a conventional U-shaped curve. The plant level at which the long run average cost is minimum will be of optimum size. For a given plant, the optimum output level will be achieved at a point where the average cost is the least. This condition can be easily verified from the short run total cost function. The level of output that a firm would like to supply to the market will depend on the price that can charge for its product. In other words, a firm’s supply is a positive function of the product price. To get the firm’s supply schedule, oneneeds to know the firm's cost function and its objectives.