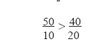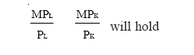INTRODUCTION
Production process involves the transformation of inputs into output. The inputs could be land, labour, capital, entrepreneurship etc. and the output could be goods or services. In a production process managers take four types of decisions:
(a) whether to produce or not,
(b) how much output to produce,
(c) what input combination to use, and
(d) what type of technology to use. This Unit deals with the analysis of managers’ decision rules concerning
(c) and (d) above.
The analysis of the other two decisions will be covered in Units of this block. In this unit, we shall begin with a general discussion of the concept of production function. The analysis of this unit mainly focuses on the firms that produce a single product. Analysis on decisions related to multiproduct firms is also given briefly. The nature of production when there is only one variable input is taken up first. We then move on to the problem of finding optimum combination of inputs for producing a particular level of output when there are two or more variable inputs. You will learn various functional forms of production frequently used by economists and their empirical estimation in Unit. The unit concludes with the production decisions in case of product mix of multiproduct firms.
PRODUCTION FUNCTION
Suppose we want to produce apples. We need land, seedlings, fertilizer, water, labour, and some machinery. These are called inputs or factors of production. The output is apples. In general a given output can be produced with different combinations of inputs. A production function is the functional relationship between inputs and output. It shows the maximum output which can be obtained for a given combination of inputs. It expresses the technological relationship between inputs and output of a product. In general, we can represent the production function for a firm as: Q = f (x1, x2, ….,xn)
Where Q is the maximum quantity of output, x1, x2, ….,xn are the quantities of various inputs, and f stands for functional relationship between inputs and output. For the sake of clarity, let us restrict our attention to only one product produced using either one input or two inputs. If there are only two inputs, capital (K) and labour (L), we write the production function as: Q = f (L, K) This function defines the maximum rate of output (Q) obtainable for a given rate of capital and labour input. It may be noted here that outputs may be tangible like computers, television sets, etc., or it may be intangible like
education, medical care, etc. Similarly, the inputs may be other than capital and labour. Also, the principles discussed in this unit apply to situations with more than two inputs as well.
Economic Efficiency and Technical Efficiency
We say that a firm is technically efficient when it obtains maximum level of output from any given combination of inputs. The production function
incorporates the technically efficient method of production. A producer cannot decrease one input and at the same time maintain the output at the same level without increasing one or more inputs. When economists use production functions, they assume that the maximum output is obtained from any given
combination of inputs. That is, they assume that production is technically efficient. On the other hand, we say a firm is economically efficient, when it produces a given amount of output at the lowest possible cost for a combination of inputs provided that the prices of inputs are given. Therefore, when only input combinations are given, we deal with the problem of technical efficiency; that is, how to produce maximum output. On the other hand, when input prices are also given in addition to the combination of inputs, we deal with the problem of economic efficiency; that is, how to produce a given amount of output at the lowest possible cost. One has to be careful while interpreting whether a production process is efficient or inefficient. Certainly a production process can be called efficient if another process produces the same level of output using one or more inputs, other things remaining constant. However, if a production process uses less of some inputs and more of others, the economically efficient method of producing a given level of output depends on the prices of inputs. Even when two production processes are technically efficient, one process may be economically efficient under one set of input prices, while the other production process may be economically efficient at other input prices. Let us take an example to differentiate between technical efficiency and economic efficiency. An ABC company is producing ready made garments using cotton fabric in a certain production process. It is found that 10 percent of fabric is wasted in that process. An engineer suggested that the wastage of fabric can be eliminated by modifying the present production process. To this suggestion, an economist reacted differently saying that if the cost of wasted fabric is less than that of modifying production process then it may not beeconomically efficient to modify the production process.
Short Run and Long Run
All inputs can be divided into two categories: i) fixed inputs and ii) variable inputs. A fixed input is one whose quantity cannot be varied during the time
under consideration. The time period will vary depending on the circumstances Although any input may be varied no matter how short the time interval, the cost involved in augmenting the amount of certain inputs is enormous; so as to make quick variation impractical. Such inputs are classified as fixed and include plant and equipment of the firm. On the other hand, a variable input is one whose amount can be changed during the relevant period. For example, in the construction business the number of workers can be increased or decreased on short notice. Many ‘builder’ firms employ workers on a daily wage basis and frequent change in the number of workers is made depending upon the need. The amount of milk that goes in the production of butter can be altered quickly and easily and is thus classified as a variable input in the production process. Whether or not an input is fixed or variable depends upon the time period involved. The longer the length of the time period under consideration, the more likely it is that the input will be variable and not fixed. Economists find it convenient to distinguish between the short run and the long run. The short run is defined to be that period of time when some of the firm’s inputs are fixed. Since it is most difficult to change plant and equipment among all inputs, the short run is generally accepted as the time interval over which the firm’s plant and equipment remain fixed. In contrast, the long run is that period over which all the firms’ inputs are variable. In other words, the firm has the flexibility to adjust or change its environment. Production processes of firms generally permit a variation in the proportion in which inputs are used. In the long run, input proportions can be varied considerably. For example, at Maruti Udyog Limited, an automobile dye can be made on conventional machine tools with more labour and less expensive equipment, or it can be made on numerically controlled machine tools with less labour and more expensive equipment i.e. the amount of labour and amount of equipment used can be varied. Later in this unit, this aspect is considered in more detail. On the other hand, there are very few production processes in which inputs have to be combined in fixed proportions. Consider, Ranbaxy or Smith-Kline-Beecham or any other pharmaceutical firm. In order to produce a drug, the firm may have to use a fixed amount of aspirin per 10 gm of the drug. Even in this case a certain (although small) amount of variation in the proportion of aspirin may be permissible. If, on the other hand, no flexibility in the ratio of inputs is possible, the technology is described as fixed proportion type. We refer to this extreme case later in this unit, but as should beapparent, it is extremely rare in practice.
PRODUCTION FUNCTION WITH ONE VARIABLE INPUT
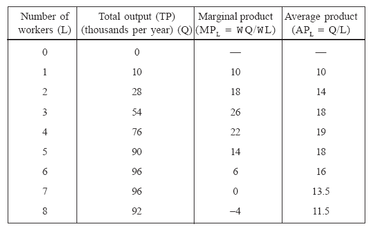
Consider the simplest two input production process - where one input with a fixed quantity and the other input with is variable quantity. Suppose that the fixed input is the service of machine tools, the variable input is labour, and the output is a metal part. The production function in this case can be represented as: Q = f (K, L) Where Q is output of metal parts, K is service of five machine tools (fixed input), and L is labour (variable input). The variable input can be combined with the fixed input to produce different levels of output. Total, Average, and Marginal Products The production function given above shows us the maximum total product (TP) that can be obtained using different combinations of quantities of inputs. Suppose the metal parts company decides to know the output level for different input levels of labour using fixed five machine tools. Table explains the total output for different levels of variable input. In this example, the TP rises with increase in labour up to a point (six workers), becomes constant betweensixth and seventh workers, and then declines.
Production process involves the transformation of inputs into output. The inputs could be land, labour, capital, entrepreneurship etc. and the output could be goods or services. In a production process managers take four types of decisions:
(a) whether to produce or not,
(b) how much output to produce,
(c) what input combination to use, and
(d) what type of technology to use. This Unit deals with the analysis of managers’ decision rules concerning
(c) and (d) above.
The analysis of the other two decisions will be covered in Units of this block. In this unit, we shall begin with a general discussion of the concept of production function. The analysis of this unit mainly focuses on the firms that produce a single product. Analysis on decisions related to multiproduct firms is also given briefly. The nature of production when there is only one variable input is taken up first. We then move on to the problem of finding optimum combination of inputs for producing a particular level of output when there are two or more variable inputs. You will learn various functional forms of production frequently used by economists and their empirical estimation in Unit. The unit concludes with the production decisions in case of product mix of multiproduct firms.
PRODUCTION FUNCTION
Suppose we want to produce apples. We need land, seedlings, fertilizer, water, labour, and some machinery. These are called inputs or factors of production. The output is apples. In general a given output can be produced with different combinations of inputs. A production function is the functional relationship between inputs and output. It shows the maximum output which can be obtained for a given combination of inputs. It expresses the technological relationship between inputs and output of a product. In general, we can represent the production function for a firm as: Q = f (x1, x2, ….,xn)
Where Q is the maximum quantity of output, x1, x2, ….,xn are the quantities of various inputs, and f stands for functional relationship between inputs and output. For the sake of clarity, let us restrict our attention to only one product produced using either one input or two inputs. If there are only two inputs, capital (K) and labour (L), we write the production function as: Q = f (L, K) This function defines the maximum rate of output (Q) obtainable for a given rate of capital and labour input. It may be noted here that outputs may be tangible like computers, television sets, etc., or it may be intangible like
education, medical care, etc. Similarly, the inputs may be other than capital and labour. Also, the principles discussed in this unit apply to situations with more than two inputs as well.
Economic Efficiency and Technical Efficiency
We say that a firm is technically efficient when it obtains maximum level of output from any given combination of inputs. The production function
incorporates the technically efficient method of production. A producer cannot decrease one input and at the same time maintain the output at the same level without increasing one or more inputs. When economists use production functions, they assume that the maximum output is obtained from any given
combination of inputs. That is, they assume that production is technically efficient. On the other hand, we say a firm is economically efficient, when it produces a given amount of output at the lowest possible cost for a combination of inputs provided that the prices of inputs are given. Therefore, when only input combinations are given, we deal with the problem of technical efficiency; that is, how to produce maximum output. On the other hand, when input prices are also given in addition to the combination of inputs, we deal with the problem of economic efficiency; that is, how to produce a given amount of output at the lowest possible cost. One has to be careful while interpreting whether a production process is efficient or inefficient. Certainly a production process can be called efficient if another process produces the same level of output using one or more inputs, other things remaining constant. However, if a production process uses less of some inputs and more of others, the economically efficient method of producing a given level of output depends on the prices of inputs. Even when two production processes are technically efficient, one process may be economically efficient under one set of input prices, while the other production process may be economically efficient at other input prices. Let us take an example to differentiate between technical efficiency and economic efficiency. An ABC company is producing ready made garments using cotton fabric in a certain production process. It is found that 10 percent of fabric is wasted in that process. An engineer suggested that the wastage of fabric can be eliminated by modifying the present production process. To this suggestion, an economist reacted differently saying that if the cost of wasted fabric is less than that of modifying production process then it may not beeconomically efficient to modify the production process.
Short Run and Long Run
All inputs can be divided into two categories: i) fixed inputs and ii) variable inputs. A fixed input is one whose quantity cannot be varied during the time
under consideration. The time period will vary depending on the circumstances Although any input may be varied no matter how short the time interval, the cost involved in augmenting the amount of certain inputs is enormous; so as to make quick variation impractical. Such inputs are classified as fixed and include plant and equipment of the firm. On the other hand, a variable input is one whose amount can be changed during the relevant period. For example, in the construction business the number of workers can be increased or decreased on short notice. Many ‘builder’ firms employ workers on a daily wage basis and frequent change in the number of workers is made depending upon the need. The amount of milk that goes in the production of butter can be altered quickly and easily and is thus classified as a variable input in the production process. Whether or not an input is fixed or variable depends upon the time period involved. The longer the length of the time period under consideration, the more likely it is that the input will be variable and not fixed. Economists find it convenient to distinguish between the short run and the long run. The short run is defined to be that period of time when some of the firm’s inputs are fixed. Since it is most difficult to change plant and equipment among all inputs, the short run is generally accepted as the time interval over which the firm’s plant and equipment remain fixed. In contrast, the long run is that period over which all the firms’ inputs are variable. In other words, the firm has the flexibility to adjust or change its environment. Production processes of firms generally permit a variation in the proportion in which inputs are used. In the long run, input proportions can be varied considerably. For example, at Maruti Udyog Limited, an automobile dye can be made on conventional machine tools with more labour and less expensive equipment, or it can be made on numerically controlled machine tools with less labour and more expensive equipment i.e. the amount of labour and amount of equipment used can be varied. Later in this unit, this aspect is considered in more detail. On the other hand, there are very few production processes in which inputs have to be combined in fixed proportions. Consider, Ranbaxy or Smith-Kline-Beecham or any other pharmaceutical firm. In order to produce a drug, the firm may have to use a fixed amount of aspirin per 10 gm of the drug. Even in this case a certain (although small) amount of variation in the proportion of aspirin may be permissible. If, on the other hand, no flexibility in the ratio of inputs is possible, the technology is described as fixed proportion type. We refer to this extreme case later in this unit, but as should beapparent, it is extremely rare in practice.
PRODUCTION FUNCTION WITH ONE VARIABLE INPUT
Consider the simplest two input production process - where one input with a fixed quantity and the other input with is variable quantity. Suppose that the fixed input is the service of machine tools, the variable input is labour, and the output is a metal part. The production function in this case can be represented as: Q = f (K, L) Where Q is output of metal parts, K is service of five machine tools (fixed input), and L is labour (variable input). The variable input can be combined with the fixed input to produce different levels of output. Total, Average, and Marginal Products The production function given above shows us the maximum total product (TP) that can be obtained using different combinations of quantities of inputs. Suppose the metal parts company decides to know the output level for different input levels of labour using fixed five machine tools. Table explains the total output for different levels of variable input. In this example, the TP rises with increase in labour up to a point (six workers), becomes constant betweensixth and seventh workers, and then declines.
Two other important concepts are the average product (AP) and the marginal product (MP) of an input. The AP of an input is the TP divided by the
amount of input used to produce this amount of output. Thus AP is the output-input ratio for each level of variable input usage. The MP of an input is
the addition to TP resulting from the addition of one unit of input, when the amounts of other inputs are constant. In our example of machine parts
production process, the AP of labour is the TP divided by the number of workers.APL = Q/L As shown in Table 7.1, the APL first rises, reaches maximum at 19, and the declines thereafter. Similarly, the MP of labour is the additional output attributable to using one additional worker with use of other input (service of five machine tools) fixed. MPL = W Q/WL Where W means ‘the change in’. For example, from Table for MP4
(marginal product of 4th worker) WQ = 76–54 = 22 and WL = 4–3 =1. Therefore, MP4 = (22/1) = 22. Note that although the MP first increases with
addition of workers, it declines later and for the addition of 8th worker it becomes negative (–4).
amount of input used to produce this amount of output. Thus AP is the output-input ratio for each level of variable input usage. The MP of an input is
the addition to TP resulting from the addition of one unit of input, when the amounts of other inputs are constant. In our example of machine parts
production process, the AP of labour is the TP divided by the number of workers.APL = Q/L As shown in Table 7.1, the APL first rises, reaches maximum at 19, and the declines thereafter. Similarly, the MP of labour is the additional output attributable to using one additional worker with use of other input (service of five machine tools) fixed. MPL = W Q/WL Where W means ‘the change in’. For example, from Table for MP4
(marginal product of 4th worker) WQ = 76–54 = 22 and WL = 4–3 =1. Therefore, MP4 = (22/1) = 22. Note that although the MP first increases with
addition of workers, it declines later and for the addition of 8th worker it becomes negative (–4).
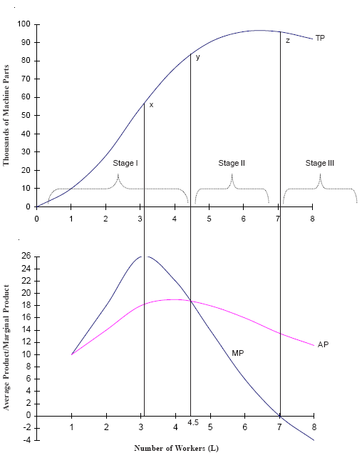
The graphical presentation of total, average, and marginal products for our example of machine parts production process is shown in FigureRelationship between TP, MP and AP Curves
Examine Table and its graphical presentation in Figure 7.1. We can establish the following relationship between TP, MP, and AP curves.
1a) If MP > 0, TP will be rising as L increases. The TP curve begins at the origin, increases at an increasing rate over the range 0 to 3, and then
increases at a decreasing rate. The MP reaches a maximum at 3, which corresponds to an inflection point (x) on the TP curve. At the inflection
point, the TP curve changes from increasing at an increasing rate to increasing at a decreasing rate.
b) If MP = 0, TP will be constant as L increases. The TP is constant between workers 6 and 7.
c) If MP < 0, TP will be declining as L increases. The TP declines beyond
7. Also, the TP curve reaches a maximum when MP = 0 and then starts declining when MP < 0.
2. MP intersects AP (MP = AP) at the maximum point on the AP curve.
This occurs at labour input rate 4.5. Also, observe that whenever MP > AP, the AP is rising (upto number of workers 4.5) — it makes no
difference whether MP is rising or falling. When MP < AP (from number of workers 4.5), the AP is falling. Therefore, the intersection must occur at the maximum point of AP. It is important to understand why. The key is that AP increases as long as the MP is greater than AP. And AP decreases as long as MP is less than AP. Since AP is positively or negatively sloped depending on whether MP is above or below AP, it follows that MP = AP at the highest point on the AP curve. This relationship between MP and AP is not unique to economics. Consider a cricket batsman, say Sachin Tendulkar, who is averaging 50 runs in 10 innings. In his next innings he scores a 100. His marginal score is 100 and his average will now be above 50. More precisely, it is 54 i.e. (50 * 10 + 100)/(10+1) = 600/11. This means when the marginal score is above the average, the average must increase. In case he had scored zero, his marginal score would be below the average, and his average would fall to 45.5 i.e. 500/11 is 45.45. Only if he had scored 50 would the average remain constant, and the marginal score would be equal to the average.
The Law of Diminishing Marginal Returns
The slope of the MP curve in Figure illustrates an important principle, the law of diminishing marginal returns. As the number of units of the variable
input increases, the other inputs held constant (fixed), there exists a point beyond which the MP of the variable input declines. Table 7.1 illustrates this
law. Observe that MP was increasing up to the addition of 4th worker (input); beyond this the MP decreases. What this law says is that MP may rise or
stay constant for some time, but as we keep increasing the units of variable input, MP should start falling. It may keep falling and turn negative, or may
stay positive all the time. Consider another example for clarity. Single application of fertilizers may increase the output by 50%, a second application
by another 30% and the third by 20% and so on. However, if you were toapply fertilizer five to six times in a year, the output may drop to zero.Three things should be noted concerning the law of diminishing marginal returns.1. This law is an empirical generalization, not a deduction from physical orbiological laws.2. It is assumed that technology remains fixed. The law of diminishingmarginal returns cannot predict the effect of an additional unit of input whentechnology is allowed to change.3. It is assumed that there is at least one input whose quantity is being heldconstant (fixed). In other words, the law of diminishing marginal returnsdoes not apply to cases where all inputs are variable.Stages of ProductionBased on the behaviour of MP and AP, economists have classified productioninto three stages:Stage 1: MP > 0, AP rising. Thus, MP > AP.Stage 2: MP > 0, but AP is falling. MP < AP but TP is increasing (becauseMP > 0).Stage 3: MP < 0. In this case TP is falling.These results are illustrated in Figure 7.1. No profit-maximising producer wouldproduce in stages I or III. In stage I, by adding one more unit of labour, theproducer can increase the AP of all units. Thus, it would be unwise on the partof the producer to stop the production in this stage. As for stage III, it doesnot pay the producer to be in this region because by reducing the labour inputthe total output can be increased and the cost of a unit of labour can be saved.Thus, the economically meaningful range is given by stage II. In Figure atthe point of inflection (x), we saw earlier that MP is maximised. At point y,since AP is maximized, we have AP = MP. At point z, TP reaches amaximum. Thus, MP = 0 at this point. If the variable input is free then theoptimum level of output is at point z where TP is maximized. However, inpractice no input will be freely available. The producer has to pay a price forit. Suppose the producer pays Rs. 200 per worker per day and the price of aunit of output (say one apple) is Rs. 10. In this case the producer will keepon hiring additional workers as long as(price of a unit of output) * (marginal product of labour) > (price of a unit oflabour)That is, marginal revenue of product (MRP) of labour > PLOn a similar analogy,(price of a unit of output) * (marginal product of capital) > (price of a unit ofcapital)That is, marginal revenue of product (MRP) of capital > PKThe left side denotes the increase in revenue and the right side denotes theincrease in the cost of adding one more unit of labour. As long as theincrement to revenues exceeds the increment to costs, the profit of theproducer will increase. As we increase the units of labour, we see that MPdiminishes. We assume that the prices of inputs and output do not change. Inthis case, as MP declines, revenues will start falling, and a point will comewhen the increase in revenue equals the increase in cost. At this point theproducer will stop adding more units of input. With further addition, since MP declines, the additional revenues would be less than the additional costs, and the profit of the producer would decline. Thus, profit maximization implies that a producer with no control over priceswill increase the use of an input until— Value of marginal product (MP) = Price of a unit of variable input
PRODUCTION FUNCTION WITH TWO VARIABLE INPUTS
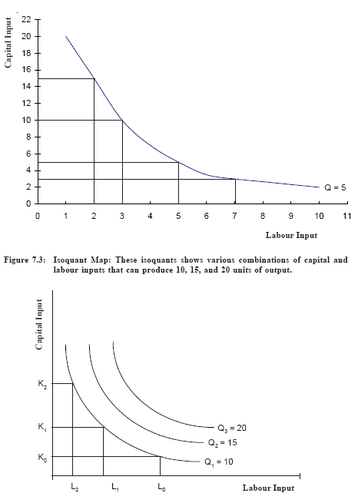
Now we turn to the case of production where two inputs (say capital andlabour) are variable. Although, we restrict our analysis to two variable inputs,all of the results hold for more than two also. We are restricting our analysisto two variable inputs because it simply allows us the scope for graphicalanalysis. When analysing production with more than one variable input, wecannot simply use sets of AP and MP curves like those discussed in section, because these curves were derived holding the use of all other inputs fixedand letting the use of only one input vary. If we change the level of fixedinput, the TP, AP and MP curves would shift. In the case of two variableinputs, changing the use of one input would cause a shift in the MP and APcurves of the other input. For example, an increase in capital would probablyresult in an increase in the MP of labour over a wide range of labour use.Production IsoquantsIn Greek the word ‘iso’ means ‘equal’ or ’same’. A production isoquant(equal output curve) is the locus of all those combinations of two inputs whichyields a given level of output. With two variable inputs, capital and labour, theisoquant gives the different combinations of capital and labour, that produces thesame level of output. For example, 5 units of output can be produced usingeither 15 units of capital (K) or 2 units of labour (L) or K=10 and L=3 or K=5and L=5 or K=3 and L=7. These four combinations of capital and labour arefour points on the isoquant associated with 5 units of output as shown in Figure. And if we assume that capital and labour are continuously divisible, therewould be many more combinations on this isoquant.Now let us assume that capital, labour, and output are continuously divisible inorder to set forth the typically assumed characteristics of isoquants. Figure illustrates three such isoquants. Isoquant I shows all the combinations ofcapital and labour that will produce 10 units of output. According to thisisoquant, it is possible to obtain this output if K0 units of capital and L0 units of
Examine Table and its graphical presentation in Figure 7.1. We can establish the following relationship between TP, MP, and AP curves.
1a) If MP > 0, TP will be rising as L increases. The TP curve begins at the origin, increases at an increasing rate over the range 0 to 3, and then
increases at a decreasing rate. The MP reaches a maximum at 3, which corresponds to an inflection point (x) on the TP curve. At the inflection
point, the TP curve changes from increasing at an increasing rate to increasing at a decreasing rate.
b) If MP = 0, TP will be constant as L increases. The TP is constant between workers 6 and 7.
c) If MP < 0, TP will be declining as L increases. The TP declines beyond
7. Also, the TP curve reaches a maximum when MP = 0 and then starts declining when MP < 0.
2. MP intersects AP (MP = AP) at the maximum point on the AP curve.
This occurs at labour input rate 4.5. Also, observe that whenever MP > AP, the AP is rising (upto number of workers 4.5) — it makes no
difference whether MP is rising or falling. When MP < AP (from number of workers 4.5), the AP is falling. Therefore, the intersection must occur at the maximum point of AP. It is important to understand why. The key is that AP increases as long as the MP is greater than AP. And AP decreases as long as MP is less than AP. Since AP is positively or negatively sloped depending on whether MP is above or below AP, it follows that MP = AP at the highest point on the AP curve. This relationship between MP and AP is not unique to economics. Consider a cricket batsman, say Sachin Tendulkar, who is averaging 50 runs in 10 innings. In his next innings he scores a 100. His marginal score is 100 and his average will now be above 50. More precisely, it is 54 i.e. (50 * 10 + 100)/(10+1) = 600/11. This means when the marginal score is above the average, the average must increase. In case he had scored zero, his marginal score would be below the average, and his average would fall to 45.5 i.e. 500/11 is 45.45. Only if he had scored 50 would the average remain constant, and the marginal score would be equal to the average.
The Law of Diminishing Marginal Returns
The slope of the MP curve in Figure illustrates an important principle, the law of diminishing marginal returns. As the number of units of the variable
input increases, the other inputs held constant (fixed), there exists a point beyond which the MP of the variable input declines. Table 7.1 illustrates this
law. Observe that MP was increasing up to the addition of 4th worker (input); beyond this the MP decreases. What this law says is that MP may rise or
stay constant for some time, but as we keep increasing the units of variable input, MP should start falling. It may keep falling and turn negative, or may
stay positive all the time. Consider another example for clarity. Single application of fertilizers may increase the output by 50%, a second application
by another 30% and the third by 20% and so on. However, if you were toapply fertilizer five to six times in a year, the output may drop to zero.Three things should be noted concerning the law of diminishing marginal returns.1. This law is an empirical generalization, not a deduction from physical orbiological laws.2. It is assumed that technology remains fixed. The law of diminishingmarginal returns cannot predict the effect of an additional unit of input whentechnology is allowed to change.3. It is assumed that there is at least one input whose quantity is being heldconstant (fixed). In other words, the law of diminishing marginal returnsdoes not apply to cases where all inputs are variable.Stages of ProductionBased on the behaviour of MP and AP, economists have classified productioninto three stages:Stage 1: MP > 0, AP rising. Thus, MP > AP.Stage 2: MP > 0, but AP is falling. MP < AP but TP is increasing (becauseMP > 0).Stage 3: MP < 0. In this case TP is falling.These results are illustrated in Figure 7.1. No profit-maximising producer wouldproduce in stages I or III. In stage I, by adding one more unit of labour, theproducer can increase the AP of all units. Thus, it would be unwise on the partof the producer to stop the production in this stage. As for stage III, it doesnot pay the producer to be in this region because by reducing the labour inputthe total output can be increased and the cost of a unit of labour can be saved.Thus, the economically meaningful range is given by stage II. In Figure atthe point of inflection (x), we saw earlier that MP is maximised. At point y,since AP is maximized, we have AP = MP. At point z, TP reaches amaximum. Thus, MP = 0 at this point. If the variable input is free then theoptimum level of output is at point z where TP is maximized. However, inpractice no input will be freely available. The producer has to pay a price forit. Suppose the producer pays Rs. 200 per worker per day and the price of aunit of output (say one apple) is Rs. 10. In this case the producer will keepon hiring additional workers as long as(price of a unit of output) * (marginal product of labour) > (price of a unit oflabour)That is, marginal revenue of product (MRP) of labour > PLOn a similar analogy,(price of a unit of output) * (marginal product of capital) > (price of a unit ofcapital)That is, marginal revenue of product (MRP) of capital > PKThe left side denotes the increase in revenue and the right side denotes theincrease in the cost of adding one more unit of labour. As long as theincrement to revenues exceeds the increment to costs, the profit of theproducer will increase. As we increase the units of labour, we see that MPdiminishes. We assume that the prices of inputs and output do not change. Inthis case, as MP declines, revenues will start falling, and a point will comewhen the increase in revenue equals the increase in cost. At this point theproducer will stop adding more units of input. With further addition, since MP declines, the additional revenues would be less than the additional costs, and the profit of the producer would decline. Thus, profit maximization implies that a producer with no control over priceswill increase the use of an input until— Value of marginal product (MP) = Price of a unit of variable input
PRODUCTION FUNCTION WITH TWO VARIABLE INPUTS
Now we turn to the case of production where two inputs (say capital andlabour) are variable. Although, we restrict our analysis to two variable inputs,all of the results hold for more than two also. We are restricting our analysisto two variable inputs because it simply allows us the scope for graphicalanalysis. When analysing production with more than one variable input, wecannot simply use sets of AP and MP curves like those discussed in section, because these curves were derived holding the use of all other inputs fixedand letting the use of only one input vary. If we change the level of fixedinput, the TP, AP and MP curves would shift. In the case of two variableinputs, changing the use of one input would cause a shift in the MP and APcurves of the other input. For example, an increase in capital would probablyresult in an increase in the MP of labour over a wide range of labour use.Production IsoquantsIn Greek the word ‘iso’ means ‘equal’ or ’same’. A production isoquant(equal output curve) is the locus of all those combinations of two inputs whichyields a given level of output. With two variable inputs, capital and labour, theisoquant gives the different combinations of capital and labour, that produces thesame level of output. For example, 5 units of output can be produced usingeither 15 units of capital (K) or 2 units of labour (L) or K=10 and L=3 or K=5and L=5 or K=3 and L=7. These four combinations of capital and labour arefour points on the isoquant associated with 5 units of output as shown in Figure. And if we assume that capital and labour are continuously divisible, therewould be many more combinations on this isoquant.Now let us assume that capital, labour, and output are continuously divisible inorder to set forth the typically assumed characteristics of isoquants. Figure illustrates three such isoquants. Isoquant I shows all the combinations ofcapital and labour that will produce 10 units of output. According to thisisoquant, it is possible to obtain this output if K0 units of capital and L0 units of
labour inputs are used. Alternately, this output can also be obtained if K1 units of capital and L1 units of labour inputs or K2 units of capital and L2 units of
labour are used. Similarly, isoquant II shows the various combinations of capital and labour that can be used to produce 15 units of output. Isoquant III
shows all combinations that can produce 20 units of output. Each capital labour combination can be on only one isoquant. That is, isoquants cannot
intersect. These isoquants are only three of an infinite number of isoquants that could be drawn. A group of isoquants is called an isoquant map. In an
isoquant map, all isoquants lying above and to the right of a given isoquant indicate higher levels of output. Thus, in Figure 7.3 isoquant II indicates a
higher level of output than isoquant I, and isoquant III indicates a higher level of output than isoquant II.In general, isoquants are determined in the following way. First, a rate of output, say Q0, is specified. Hence the production function can be written as Q0 = f (K,L) Those combinations of K and L that satisfy this equation define the isoquant for output rate Q0.
Marginal Rate of Technical Substitution
As we have seen above, generally there are a number of ways (combinations of inputs) that a particular output can be produced. The rate, at which one
input can be substituted for another input, if output remains constant, is called the marginal rate of technical substitution (MRTS). It is defined in case of
two inputs, capital and labour, as the amount of capital that can be replaced by an extra unit of labour, without affecting total output. L MRTSL for K ΔK =Δ It is customary to define the MRTS as a positive number, since WK/WL, the slope of the isoquant, is negative. Over the relevant range of production the MRTS diminishes. That is, more and more labour is substituted for capital while holding output constant, the absolute value of WK/WL decreases. For
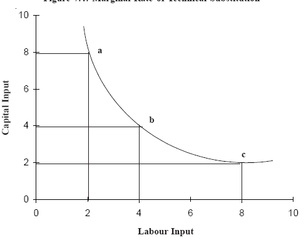
example, let us assume that 10 pairs of shoes can be produced using either 8 units of capital and 2 units of labour or 4 units each of capital and of labour
or 2 units of capital and 8 units of labour. From Figure 7.4 the MRTS of labour for capital between points a and b is equal to WK/WL = (4–8) / (4–2)
= –4/2 = –2 or | 2 |. Between points b and c, the MRTS is equal to –2/4 =\ –½ or | ½ |. The MRTS has decreased because capital and labour are not
perfect substitutes for each other. Therefore, as more of labour is added, less of capital can be used (in exchange for another unit of labour) while keepingthe output level constant.
labour are used. Similarly, isoquant II shows the various combinations of capital and labour that can be used to produce 15 units of output. Isoquant III
shows all combinations that can produce 20 units of output. Each capital labour combination can be on only one isoquant. That is, isoquants cannot
intersect. These isoquants are only three of an infinite number of isoquants that could be drawn. A group of isoquants is called an isoquant map. In an
isoquant map, all isoquants lying above and to the right of a given isoquant indicate higher levels of output. Thus, in Figure 7.3 isoquant II indicates a
higher level of output than isoquant I, and isoquant III indicates a higher level of output than isoquant II.In general, isoquants are determined in the following way. First, a rate of output, say Q0, is specified. Hence the production function can be written as Q0 = f (K,L) Those combinations of K and L that satisfy this equation define the isoquant for output rate Q0.
Marginal Rate of Technical Substitution
As we have seen above, generally there are a number of ways (combinations of inputs) that a particular output can be produced. The rate, at which one
input can be substituted for another input, if output remains constant, is called the marginal rate of technical substitution (MRTS). It is defined in case of
two inputs, capital and labour, as the amount of capital that can be replaced by an extra unit of labour, without affecting total output. L MRTSL for K ΔK =Δ It is customary to define the MRTS as a positive number, since WK/WL, the slope of the isoquant, is negative. Over the relevant range of production the MRTS diminishes. That is, more and more labour is substituted for capital while holding output constant, the absolute value of WK/WL decreases. For
example, let us assume that 10 pairs of shoes can be produced using either 8 units of capital and 2 units of labour or 4 units each of capital and of labour
or 2 units of capital and 8 units of labour. From Figure 7.4 the MRTS of labour for capital between points a and b is equal to WK/WL = (4–8) / (4–2)
= –4/2 = –2 or | 2 |. Between points b and c, the MRTS is equal to –2/4 =\ –½ or | ½ |. The MRTS has decreased because capital and labour are not
perfect substitutes for each other. Therefore, as more of labour is added, less of capital can be used (in exchange for another unit of labour) while keepingthe output level constant.
labour (namely, WL * MPL) should match the decrease in output due to a decrease of WK units of capital (namely, WK * MPK). In other words, along
an isoquant, WL * MPL = WK * MPk which is equal to
an isoquant, WL * MPL = WK * MPk which is equal to
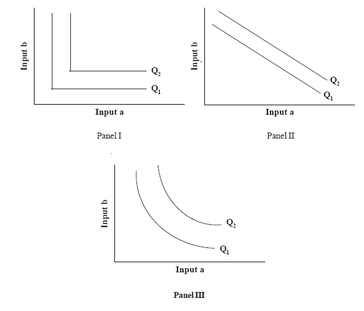
There are vast differences among inputs in how readily they can be substituted for one another. For example, in some extreme production process, one input can perfectly be substituted for another; whereas in some other extreme production process no substitution is possible. On the other hand, in most of the production processes what we see is imperfect substitution of inputs. These three general shapes that an isoquant might have are shown in Figure . In panel I, the isoquants are right angles implying that the two inputs a and b must be used in fixed proportion and they are not at all substitutable. For
instance, there is no substitution possible between the tyres and a battery in an automobile production process. The MRTS in all such cases would, therefore, be zero. The other extreme case would be where the inputs a and b are perfect substitutes as shown in panel II. The isoquants in this category will be a straight line with constant slope or MRTS. A good example of this type
instance, there is no substitution possible between the tyres and a battery in an automobile production process. The MRTS in all such cases would, therefore, be zero. The other extreme case would be where the inputs a and b are perfect substitutes as shown in panel II. The isoquants in this category will be a straight line with constant slope or MRTS. A good example of this type
would be natural gas and fuel oil, which are close substitutes in energy production. The most common situation is presented in panel III. The inputs
are imperfect substitutes in this case and the rate at which input a can be given up in return for one more unit of input b keeping the output constant
diminishes as the amount of input b increases.
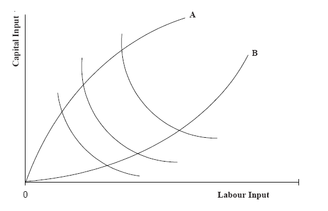
The Economic Region of Production
Isoquants may also have positively sloped segments, or bend back upon themselves, as shown in Figure . Above OA and below OB, the slope of
the isoquants is positive, which implies that increase in both capital and labour are required to maintain a certain output rate. If this is the case, the MP of one or other input must be negative. Above OA, the MP of capital is negative. Thus output will increase if less capital is used, while the amount of
labour is held constant. Below OB, the MP of labour is negative. Thus, output will increase if less labour is used, while the amount of capital is held
constant. The lines OA and OB are called ridge lines. And the region bounded by these ridge lines is called economic region of production. This means the region of production beyond the ridge lines is economically inefficient.
are imperfect substitutes in this case and the rate at which input a can be given up in return for one more unit of input b keeping the output constant
diminishes as the amount of input b increases.
The Economic Region of Production
Isoquants may also have positively sloped segments, or bend back upon themselves, as shown in Figure . Above OA and below OB, the slope of
the isoquants is positive, which implies that increase in both capital and labour are required to maintain a certain output rate. If this is the case, the MP of one or other input must be negative. Above OA, the MP of capital is negative. Thus output will increase if less capital is used, while the amount of
labour is held constant. Below OB, the MP of labour is negative. Thus, output will increase if less labour is used, while the amount of capital is held
constant. The lines OA and OB are called ridge lines. And the region bounded by these ridge lines is called economic region of production. This means the region of production beyond the ridge lines is economically inefficient.
THE OPTIMAL COMBINATION OF INPUTS
In the above section you have learned that any desired level of output can be produced using a number of different combinations of inputs. As said earlier in the introduction of this unit one of the decision problems that concerns a production process manager is, which input combination to use. That is, what
is the optimal input combination? While all the input combinations are technically efficient, the final decision to employ a particular input combination
is purely an economic decision and rests on cost (expenditure). Thus, the production manager can make either of the following two input choice
decisions:
1. Choose the input combination that yields the maximum level of output with a
given level of expenditure.
2. Choose the input combination that leads to the lowest cost of producing agiven level of output.
Thus, the decision is to minimize cost subject to an output constraint or maximize the output subject to a cost constraint. We will now discuss these
two fundamental principles. Before doing this we will introduce the concept isocost, which shows all combinations of inputs that can be used for a given
cost.
Isocost Lines
Recall that a universally accepted objective of any firm is to maximise profit. If the firm maximises profit, it will necessarily minimise cost for producing a given level of output or maximise output for a given level of cost. Suppose there are 2 inputs: capital (K) and labour (L) that are variable in the relevant
time period. What combination of (K,L) should the firm choose in order to maximise output for a given level of cost?
If there are 2 inputs, K,L, then given the price of capital (Pk) and the price of labour (PL), it is possible to determine the alternative combinations of (K,L) that can be purchased for a given level of expenditure. Suppose C is total
expenditure, then C= PL* L + Pk* KThis linear function can be plotted on a graph.
In the above section you have learned that any desired level of output can be produced using a number of different combinations of inputs. As said earlier in the introduction of this unit one of the decision problems that concerns a production process manager is, which input combination to use. That is, what
is the optimal input combination? While all the input combinations are technically efficient, the final decision to employ a particular input combination
is purely an economic decision and rests on cost (expenditure). Thus, the production manager can make either of the following two input choice
decisions:
1. Choose the input combination that yields the maximum level of output with a
given level of expenditure.
2. Choose the input combination that leads to the lowest cost of producing agiven level of output.
Thus, the decision is to minimize cost subject to an output constraint or maximize the output subject to a cost constraint. We will now discuss these
two fundamental principles. Before doing this we will introduce the concept isocost, which shows all combinations of inputs that can be used for a given
cost.
Isocost Lines
Recall that a universally accepted objective of any firm is to maximise profit. If the firm maximises profit, it will necessarily minimise cost for producing a given level of output or maximise output for a given level of cost. Suppose there are 2 inputs: capital (K) and labour (L) that are variable in the relevant
time period. What combination of (K,L) should the firm choose in order to maximise output for a given level of cost?
If there are 2 inputs, K,L, then given the price of capital (Pk) and the price of labour (PL), it is possible to determine the alternative combinations of (K,L) that can be purchased for a given level of expenditure. Suppose C is total
expenditure, then C= PL* L + Pk* KThis linear function can be plotted on a graph.
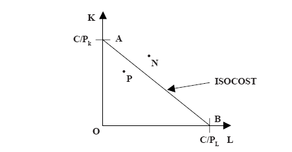
If only capital is purchased, then the maximum amount that can be bought is C/Pk shown by point A in figure . If only labour is purchased, then the
maximum amount of labour that can be purchased is C/PL shown by point B in the figure. The 2 points A and B can be joined by a straight line. This straight line is called the isocost line or equal cost line. It shows the alternative combinations of (K,L) that can be purchased for the given expenditure level C.Any point to the right and above the isocost is not attainable as it involves a level of expenditure greater than C and any point to the left and below the isocost such as P is attainable, although it implies the firm is spending less than C. You should verify that the slope of the isocost is1
EXAMPLE :
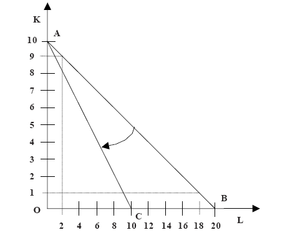
Consider the following data:
PL = 10, Pk = 20 Total Expenditure = 200.
Let us first plot the various combinations of K and L that are possible. We consider only the case when the firm spends the entire budget of 200. The
alternative combinations are shown in the figure
The slope of this isocost is –½. What will happen if labour becomes more expensive say PL increases to 20? Obviously with the same budget the firm
can now purchase lesser units of labour. The isocost still meets the Y–axis at point A (because the price of capital is unchanged), but shifts inwards in the
direction of the arrow to meet the X-axis at point C. The slope therefore changes to –1. You should work out the effect on the isocost curve on the
following:
(i) decrease in the price of labour
(ii) increase in the price of capital
(iii) decrease in the price of capital
(iv) increase in the firms budget with no change in the price of labour and capital
[Hint: The slope of the isocost will not change in this case]
Optimal Combination of Inputs: The Long Run
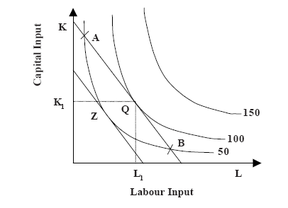
When both capital and labour are variable, determining the optimal input rates of capital and labour requires the technical information from the production function i.e. the isoquants be combined with market data on input prices i.e. the isocost function. If we superimpose the relevant isocost curve on the firm’s isoquant map, we can readily determine graphically as to which combination of inputs maximise the output for a given level of expenditure. Consider the problem of minimising the cost of a given rate of output. Specifically if the firm wants to produce 50 units of output at minimum cost. Two production isoquants have been drawn in Figure . Three possible combinations (amongst a number of more combinations) are indicated by points A, Z and B in Figure. Obviously, the firm should pick the point on the lower isocost i.e point Z. In fact, Z is the minimum cost combination of capital and labour. At Z the isocost is tangent to the 50 unit isoquant.Alternatively, consider the problem of maximising output subject to a given cost amount. You should satisfy yourself that among all possible output levels, the maximum amount will be represented by the isoquant that is tangent to the relevant isocost line. Suppose the budget of the firm increases to the amount shown by the higher of the two isocost lines in Figure 7.9, point Q or 100 units of output is the maximum attainable given the new cost constraint in Figure
can now purchase lesser units of labour. The isocost still meets the Y–axis at point A (because the price of capital is unchanged), but shifts inwards in the
direction of the arrow to meet the X-axis at point C. The slope therefore changes to –1. You should work out the effect on the isocost curve on the
following:
(i) decrease in the price of labour
(ii) increase in the price of capital
(iii) decrease in the price of capital
(iv) increase in the firms budget with no change in the price of labour and capital
[Hint: The slope of the isocost will not change in this case]
Optimal Combination of Inputs: The Long Run
When both capital and labour are variable, determining the optimal input rates of capital and labour requires the technical information from the production function i.e. the isoquants be combined with market data on input prices i.e. the isocost function. If we superimpose the relevant isocost curve on the firm’s isoquant map, we can readily determine graphically as to which combination of inputs maximise the output for a given level of expenditure. Consider the problem of minimising the cost of a given rate of output. Specifically if the firm wants to produce 50 units of output at minimum cost. Two production isoquants have been drawn in Figure . Three possible combinations (amongst a number of more combinations) are indicated by points A, Z and B in Figure. Obviously, the firm should pick the point on the lower isocost i.e point Z. In fact, Z is the minimum cost combination of capital and labour. At Z the isocost is tangent to the 50 unit isoquant.Alternatively, consider the problem of maximising output subject to a given cost amount. You should satisfy yourself that among all possible output levels, the maximum amount will be represented by the isoquant that is tangent to the relevant isocost line. Suppose the budget of the firm increases to the amount shown by the higher of the two isocost lines in Figure 7.9, point Q or 100 units of output is the maximum attainable given the new cost constraint in Figure
Regardless of the production objective, efficient production requires that the isoquant be tangent to the isocost function. If the problem is to maximise
output, subject to a cost constraint or to minimise cost for a given level of output, the same efficiency condition holds true in both situations. Intuitively, if it is possible to substitute one input for another to keep output constant while reducing total cost, the firm is not using the least cost combination of inputs. In such a situation, the firm should substitute one input for another. For example, if an extra rupee spent on capital generates more output than an extra rupee spent on labour, then more capital and less labour should be employed. At point Q in Figure , the marginal product of capital per rupee
spent on capital is equal to the marginal product of labour per rupee spent on labour. Mathematically this can be shown as
output, subject to a cost constraint or to minimise cost for a given level of output, the same efficiency condition holds true in both situations. Intuitively, if it is possible to substitute one input for another to keep output constant while reducing total cost, the firm is not using the least cost combination of inputs. In such a situation, the firm should substitute one input for another. For example, if an extra rupee spent on capital generates more output than an extra rupee spent on labour, then more capital and less labour should be employed. At point Q in Figure , the marginal product of capital per rupee
spent on capital is equal to the marginal product of labour per rupee spent on labour. Mathematically this can be shown as
possibilities that input substitutions will reduce costs. Let us work with numbers. Suppose PL = 10, Pk = 20,
MPL = 50 and MPk = 40. Thus, we have
MPL = 50 and MPk = 40. Thus, we have
This cannot be an efficient input combination, because the firm is getting more output per rupee spent on labour than on capital. If one unit of capital is sold to obtain 2 units of labour (Pk = 20, PL = 10), net increase in output will be 602. Thus the substitution of labour for capital would result in a net increase in output at no additional cost. The inefficient combination corresponds to a point such as A in Figure . At that point two much capital is employed. The firm, in order to maxmise profits will move down the isocost line by substituting labour for capital until it reaches point Q. Conversely, at a point such as B in figure the reverse is true - there is too much labour and the inequality
This means that the firm generates more output per rupee spent on capital than from rupees spent on labour. Thus a profit maximising firm should substitute capital for labour. Suppose the firm was operating at point B in Figure . If the problem is to minimise cost for a given level of output (B is on the isoquant that corresponds to 50 units of output), the firm should move from B to Z along the 50-unit isoquant thereby reducing cost, while maintaining output at 50. Alternatively, if the firm wants to maximise output for given cost, it should more from B to Q, where the isocost is tangent to the 100-unit isoquant. In this case output will increase from 50 to 100 at no additional cost. Thus both the following
decisions:
(a) the input combination that yields the maximum level of output with a given level of expenditure, and
(b) the input combination that leads to the lowest cost of producing a given level of output are satisfied at point Q in Figure .
You should be satisfied that this is indeed the case. The isocost-isoquant framework described above lends itself to various applications. It demonstrates, simply and elegantly, when relative prices of inputs change, managers will respond by substituting the input that has become relatively less expensive for the input that has become relatively more expensive. On average, we know that compared to developed countries like the US, UK, Japan and Germany, labour in India is less expensive. It is not surprising therefore to find production techniques that on average, use more labour per unit of capital in India than in the developed world. For example, in construction activity you see around you in your city, inexpensive workers do the job that in developed countries is performed by machines.One application of the isocost-isoquant framework frequently cited is the response of industry to the rapidly rising prices of energy products in the 1970s. (Remember the oil price shock of 1973 and again of 1979). Most prices of petrol and petroleum products increased across the world, and as our analysis suggests, firms responded by conserving energy by substituting other inputs for energy.RETURNS TO SCALE
Another important attribute of production function is how output responds in thelong run to changes in the scale of the firm i.e. when all inputs are increasedin the same proportion (by say 10%), how does output change. Clearly, thereare 3 possibilities. If output increases by more than an increase in inputs (i.e.by more than 10%), then the situation is one of increasing returns to scale(IRS). If output increases by less than the increase in inputs, then it is a caseof decreasing returns to scale (DRS). Lastly, output may increase byexactly the same proportion as inputs. For example a doubling of inputs maylead to a doubling of output. This is a case of constant returns to scale(CRS).
decisions:
(a) the input combination that yields the maximum level of output with a given level of expenditure, and
(b) the input combination that leads to the lowest cost of producing a given level of output are satisfied at point Q in Figure .
You should be satisfied that this is indeed the case. The isocost-isoquant framework described above lends itself to various applications. It demonstrates, simply and elegantly, when relative prices of inputs change, managers will respond by substituting the input that has become relatively less expensive for the input that has become relatively more expensive. On average, we know that compared to developed countries like the US, UK, Japan and Germany, labour in India is less expensive. It is not surprising therefore to find production techniques that on average, use more labour per unit of capital in India than in the developed world. For example, in construction activity you see around you in your city, inexpensive workers do the job that in developed countries is performed by machines.One application of the isocost-isoquant framework frequently cited is the response of industry to the rapidly rising prices of energy products in the 1970s. (Remember the oil price shock of 1973 and again of 1979). Most prices of petrol and petroleum products increased across the world, and as our analysis suggests, firms responded by conserving energy by substituting other inputs for energy.RETURNS TO SCALE
Another important attribute of production function is how output responds in thelong run to changes in the scale of the firm i.e. when all inputs are increasedin the same proportion (by say 10%), how does output change. Clearly, thereare 3 possibilities. If output increases by more than an increase in inputs (i.e.by more than 10%), then the situation is one of increasing returns to scale(IRS). If output increases by less than the increase in inputs, then it is a caseof decreasing returns to scale (DRS). Lastly, output may increase byexactly the same proportion as inputs. For example a doubling of inputs maylead to a doubling of output. This is a case of constant returns to scale(CRS).
In unit 9 we will examine returns to scale from the point of view of cost and also advance reasons for increasing and decreasing returns to scale. For the
moment consider the following example. A box with dimensions 4*4*4 has a capacity of 64 times a box with dimensions 1*1*1, even though the former
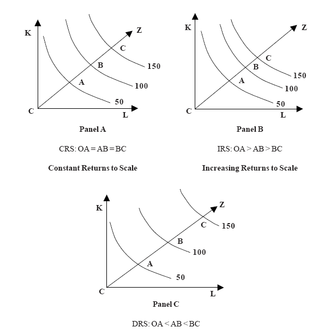
uses only 16 times more wood than the smaller box.3 Isoquants can also be used to depict returns to scale (Figure) Panel A shows constant returns to scale. Three isoquants with output levels 50,100 and 150 are drawn. In the figure, successive isoquants are equidistant from one another along the ray 0Z. Panel B shows increasing returns to scale, where the distance between 2 isoquants becomes less and less i.e. in order to double output from 50 to 100, input increase is less than double. The explanation for panel C, which exhibits decreasing returns to scale, is
analogous. There is no universal answer to which industries will show what kind of returns to scale. Some industries like public utilities (Telecom and Electricity generation) show increasing returns over large ranges of output, whereas other industries exhibit constant or even decreasing returns to scale over the relevant output range. Therefore, whether an industry has constant, increasing or decreasing returns to scale is largely an empirical issue.
moment consider the following example. A box with dimensions 4*4*4 has a capacity of 64 times a box with dimensions 1*1*1, even though the former
uses only 16 times more wood than the smaller box.3 Isoquants can also be used to depict returns to scale (Figure) Panel A shows constant returns to scale. Three isoquants with output levels 50,100 and 150 are drawn. In the figure, successive isoquants are equidistant from one another along the ray 0Z. Panel B shows increasing returns to scale, where the distance between 2 isoquants becomes less and less i.e. in order to double output from 50 to 100, input increase is less than double. The explanation for panel C, which exhibits decreasing returns to scale, is
analogous. There is no universal answer to which industries will show what kind of returns to scale. Some industries like public utilities (Telecom and Electricity generation) show increasing returns over large ranges of output, whereas other industries exhibit constant or even decreasing returns to scale over the relevant output range. Therefore, whether an industry has constant, increasing or decreasing returns to scale is largely an empirical issue.