Common Descriptive Statistics for Quantitative Data
Measures of central tendency:
Excel Formulas
Mean: =average(data_range)
Median: =median(data_range)
Variance: =var(data_range)
Standard deviation: = stdev(data_range)
Range: =max(data_range) – min(data_range)
IQR = range containing the middle 50% of the data = percentile(data_range,.75) – percentile(data_range,.25)
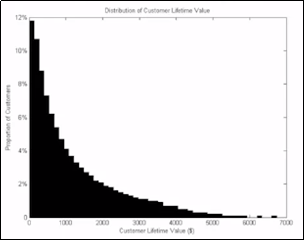
Examining a customer portfolio
An analysis of subscribers to a large US telecom provider:
Examples of correlation:
The middle plot that has an r value of 0.9, very high correlation there, very tight cluster, looks like pretty much a straight line.
When we have a lower correlation coefficient, the 0.4 on the right, or the negative 0.7, we see there's more dispersion there. But there still is a linear relationship.
Correlation can, however, be misleading.
1. This is due to outliers.
If we try to draw a best fitting line for the scatter plot below, we will be shown that there is a strong linear relationship here. But actually, it is because of that one single outlier that we will get that result. If we were to discard that and just look at that mass of points, we would not get nearly as strong a linear relationship.
2. Non-linearity
In this case, if we look at the lower right, we have a correlation of zero. This doesn't mean that there's no relationship between X and Y. It means that there's not a linear relationship between X and Y. This relationship is a negative quadratic relationship, so Y is related to X-squared. It’s a very strong quadratic relationship, but it's not a linear relationship. That's why we're getting the correlation of zero.
- Mean – the average value
- Median – the “middle” value – unlike the mean, the median is not sensitive to extreme values
- Standard deviation
- Variance
- Range
- Inter-quartile range (IQR)
Excel Formulas
Mean: =average(data_range)
Median: =median(data_range)
Variance: =var(data_range)
Standard deviation: = stdev(data_range)
Range: =max(data_range) – min(data_range)
IQR = range containing the middle 50% of the data = percentile(data_range,.75) – percentile(data_range,.25)
Examining a customer portfolio
An analysis of subscribers to a large US telecom provider:
Examples of correlation:
The middle plot that has an r value of 0.9, very high correlation there, very tight cluster, looks like pretty much a straight line.
When we have a lower correlation coefficient, the 0.4 on the right, or the negative 0.7, we see there's more dispersion there. But there still is a linear relationship.
Correlation can, however, be misleading.
1. This is due to outliers.
If we try to draw a best fitting line for the scatter plot below, we will be shown that there is a strong linear relationship here. But actually, it is because of that one single outlier that we will get that result. If we were to discard that and just look at that mass of points, we would not get nearly as strong a linear relationship.
2. Non-linearity
In this case, if we look at the lower right, we have a correlation of zero. This doesn't mean that there's no relationship between X and Y. It means that there's not a linear relationship between X and Y. This relationship is a negative quadratic relationship, so Y is related to X-squared. It’s a very strong quadratic relationship, but it's not a linear relationship. That's why we're getting the correlation of zero.
