Perspective Analytics (Maximize Revenue and Market Structure Competitions)
What is Prescriptive Analytics?Descriptive analytics takes data, collects it, and tries to map the data to patterns that you can understand in the data.
Predictive analytics try to take the behavior of consumers and predict from their past behavior what they're going to do in the future.
With prescriptive analytics, we're going to try to give a recommendation.
We say that given the prediction that we had before and given the description of how consumers interact with companies and with other consumers, can we give a recommendation on what the company needs to do in order to change the behavior of consumers.
Defining a problemA problem we would like to solve will typically have a set of goals we want to achieve, a set of actions we can take to achieve this goal and a model, which describes how the actions impact the goal.
The way to map how actions influence the goal is called the model.
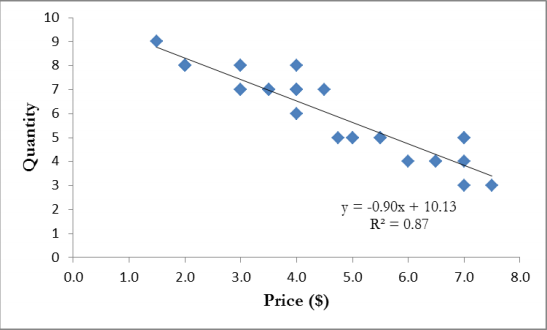
Example 1: Optimal price to sell maximum quantity
Question asked about the data: “how can we maximize the quantity of the product sold?”.
In this example, the goal is to “maximize quantity sold”.
The action we can take is to change the price to encourage consumers to buy the product.
Model here is the regression model which shows us that if the price is increased by $1, how much will the demand go down by.
The question here is, can we change the price even more to do better? Can we use some sort of prediction or recommendation to give to the company to say, can we increase the quantity sold? à Yes. We can probably give them the product for free. We can actually set the price to be 0.
This can be done by plugging in x=0 and we get the value of 10.13 which is the maximum quantity we can sell.
Example 2: Maximize revenue
The goal in this problem is to receive the highest revenue possible, or to maximize revenue.
The possible action (again) is setting different prices for the product.
How does setting a price change the revenue from selling product?
Here, we need a model to describe what is the relationship between setting prices and setting quantities of product, to generating revenue by a company.
There are two “forces” in operation when we change the price.
Now, the question is, how can we find the price that generates the maximum revenue for us?
The revenue from a product is the multiplication of the number of items sold by the price of each item.
Let us assume that the demands follows the regression equation:
In the above table, it is easy to find the demand which gives maximum revenue.
But in the general case, problems can be very hard to solve. A lot of variables to change, many actions to take, many it's not a discrete. One way we can do it and solve it, is try to take a graphical approach, and find where the maximum revenue is.
As we can see, the maximum revenue is generated at the price of approximately $5.50.
Example 3: Maximizing profits
In many cases a firm is not interested in maximizing its revenues. It wants to make sure that after paying for the cost of production of the items, it still has money left in the bank.
We now must take into consideration the cost of producing the items.
Our goal is to maximize profit, or in other words, maximize revenues minus costs.
Suppose each product in the same model we've discussed before costs $2 to produce. What we can do is we can take the same graph of revenue we created before, and for each price point on the x-axis we now add a point of the total cost it would cost us to produce those number of items we're setting.
We can plot a new graph.
We can see that the price of roughly $6.5 we're going to maximize the profit.
The question now is: Can we find the way to find where the maximum profit is without having to actually calculate the profit and calculate those, and draw these graphs for every combination of prices?
Let's take a look at the different forces operating in this type of problem.
What does optimization (maximizing profits) do?
Optimization (“finding the best price to maximize profit”) tries to increase price until the there is no additional gain in profit.
Example: If we increase price from 1.5 to 2.0, the revenue will increase by 16.66-13.17 = 3.49, while the cost will decrease by 0.9. Therefore the increase is profit is positive, and it is worthwhile to increase the price.
Example: What happens if we increase the price from 6.5 to 7.0?
We see that we're slowly increasing the price in which we get a different increase or decrease in profit. The question now is how far should we increase the price and find optimal profit? How far or how high should we set the price to say stop here? This is the optimal profit.
The idea is that you just increase until the change in profit is 0, until it turns from positive to negative. We can look at the change in revenue and at the change in profit. When they're equal, when the increase in revenue = the increase in cost, or decrease in revenue = decrease in cost, then we say that this is the optimal profit. This principle is called the marginal revenue equals the marginal cost principle.
Predictive analytics try to take the behavior of consumers and predict from their past behavior what they're going to do in the future.
With prescriptive analytics, we're going to try to give a recommendation.
We say that given the prediction that we had before and given the description of how consumers interact with companies and with other consumers, can we give a recommendation on what the company needs to do in order to change the behavior of consumers.
Defining a problemA problem we would like to solve will typically have a set of goals we want to achieve, a set of actions we can take to achieve this goal and a model, which describes how the actions impact the goal.
The way to map how actions influence the goal is called the model.
Example 1: Optimal price to sell maximum quantity
Question asked about the data: “how can we maximize the quantity of the product sold?”.
In this example, the goal is to “maximize quantity sold”.
The action we can take is to change the price to encourage consumers to buy the product.
Model here is the regression model which shows us that if the price is increased by $1, how much will the demand go down by.
The question here is, can we change the price even more to do better? Can we use some sort of prediction or recommendation to give to the company to say, can we increase the quantity sold? à Yes. We can probably give them the product for free. We can actually set the price to be 0.
This can be done by plugging in x=0 and we get the value of 10.13 which is the maximum quantity we can sell.
Example 2: Maximize revenue
The goal in this problem is to receive the highest revenue possible, or to maximize revenue.
The possible action (again) is setting different prices for the product.
How does setting a price change the revenue from selling product?
Here, we need a model to describe what is the relationship between setting prices and setting quantities of product, to generating revenue by a company.
There are two “forces” in operation when we change the price.
- When the price is decreased, the quantity sold is higher, but the revenue for each item sold is lower.
- When the price is increased, we make more money for each item sold, but we sell less items.
Now, the question is, how can we find the price that generates the maximum revenue for us?
The revenue from a product is the multiplication of the number of items sold by the price of each item.
Let us assume that the demands follows the regression equation:
In the above table, it is easy to find the demand which gives maximum revenue.
But in the general case, problems can be very hard to solve. A lot of variables to change, many actions to take, many it's not a discrete. One way we can do it and solve it, is try to take a graphical approach, and find where the maximum revenue is.
As we can see, the maximum revenue is generated at the price of approximately $5.50.
Example 3: Maximizing profits
In many cases a firm is not interested in maximizing its revenues. It wants to make sure that after paying for the cost of production of the items, it still has money left in the bank.
We now must take into consideration the cost of producing the items.
Our goal is to maximize profit, or in other words, maximize revenues minus costs.
Suppose each product in the same model we've discussed before costs $2 to produce. What we can do is we can take the same graph of revenue we created before, and for each price point on the x-axis we now add a point of the total cost it would cost us to produce those number of items we're setting.
- One the left-hand side, you can see that the red dot is higher than the blue does, where actually the profit there is negative.
- Towards the right-hand side of the graph when we're increasing price and the revenue, the blue dots, go up and up, costs also go down because the quantities we're setting go lower.
- At some point, and this is where the green arrow is, we're maximizing our profit, which is basically the distance or the difference between the revenues and the cost.
We can plot a new graph.
We can see that the price of roughly $6.5 we're going to maximize the profit.
The question now is: Can we find the way to find where the maximum profit is without having to actually calculate the profit and calculate those, and draw these graphs for every combination of prices?
Let's take a look at the different forces operating in this type of problem.
- Selling too cheaply yields a negative profit. There's actually a minimum amount you want to sell in order to make a profit from your company.
- The optimal price we found that generates the maximum profit is different than the price we found that generates the maximum revenue - it is now 6.5 for profits instead of 5.5 as for revenue.
- Is this a principle we can always apply? Do higher costs mean the optimal price is higher?
What does optimization (maximizing profits) do?
Optimization (“finding the best price to maximize profit”) tries to increase price until the there is no additional gain in profit.
Example: If we increase price from 1.5 to 2.0, the revenue will increase by 16.66-13.17 = 3.49, while the cost will decrease by 0.9. Therefore the increase is profit is positive, and it is worthwhile to increase the price.
Example: What happens if we increase the price from 6.5 to 7.0?
- Revenue increases by 26.81-27.82=-1.01
- Cost increases by 7.66-8.56 = -0.9
- Total gain in profit is -1.01 - (-0.9) = -0.11
We see that we're slowly increasing the price in which we get a different increase or decrease in profit. The question now is how far should we increase the price and find optimal profit? How far or how high should we set the price to say stop here? This is the optimal profit.
The idea is that you just increase until the change in profit is 0, until it turns from positive to negative. We can look at the change in revenue and at the change in profit. When they're equal, when the increase in revenue = the increase in cost, or decrease in revenue = decrease in cost, then we say that this is the optimal profit. This principle is called the marginal revenue equals the marginal cost principle.
